Questões de Concurso
Filtrar
270 Questões de concurso encontradas
Página 13 de 54
Questões por página:
Questões por página:
Em uma agência de um banco comercial,20% das contas-correntes são contas conjuntas, isto é, contas que possuem dois ou mais titulares.
Considerando-se que um gerente dessa agência administra 4 contas, qual é a probabilidade de que a maioria das contas que esse gerente administra sejam contas conjuntas?
Considerando-se que um gerente dessa agência administra 4 contas, qual é a probabilidade de que a maioria das contas que esse gerente administra sejam contas conjuntas?
Concurso:
Banco da Amazônia
Disciplina:
Estatística
Uma empresa adota cinco faixas salariais entre os seus funcionários. A Tabela a seguir representa a distribuição do número de funcionários em cada faixa salarial (FS). A última coluna da Tabela representa a distribuição acumulada do número de funcionários nas faixas menores ou iguais a FS.
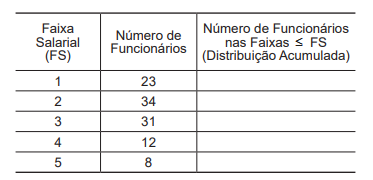
Os valores da última coluna dessa Tabela são
Concurso:
SEDUC-MT
Disciplina:
Estatística
O poder de um teste de hipóteses é definido pela probabilidade de:
Concurso:
SEDUC-MT
Disciplina:
Estatística
O coeficiente de assimetria da distribuição da média amostral, aproximadamente, considerando o Teorema Central do Limite, quando o tamanho da amostra cresce, é igual a:
Concurso:
SEDUC-MT
Disciplina:
Estatística
Considere S um espaço amostral. Uma probabilidade é uma função P que associa a cada subconjunto de S (evento) um número real.
Com base nisso, pode-se dizer que a probabilidade:
Com base nisso, pode-se dizer que a probabilidade: