Questões de Concurso
Filtrar
270 Questões de concurso encontradas
Página 20 de 54
Questões por página:
Questões por página:
Um andarilho pode chegar a determinado destino (C) partindo de uma origem A ou B. A probabilidade de ele chegar em C a partir de A é representada pela probabilidade condicional P(C|A) = 0,3, enquanto a probabilidade de ele chegar em C a partir de B é representada pela probabilidade condicional P(C|A) = 0,2.
Considerando-se a situação hipotética apresentada, e ainda que P(A) = P(B) = 0,5, é correto afirmar que P(C) é igual a
Considerando-se a situação hipotética apresentada, e ainda que P(A) = P(B) = 0,5, é correto afirmar que P(C) é igual a
Concurso:
PC-RO
Disciplina:
Estatística
As pessoas que cumprem penas judiciais em determinado município são classificadas como reincidentes (R) ou não reincidentes (Rc ). Além disso, essas mesmas pessoas são classificadas de acordo com o tipo do regime no cumprimento da pena: regime fechado (F) ou regime não fechado (Fc ).
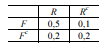
Considerando-se que a tabela precedente mostra a distribuição de probabilidade conjunta dos eventos apresentados na situação hipotética anterior, é correto afirmar que o valor da probabilidade condicional P(R|F) é igual a

Considerando-se que a tabela precedente mostra a distribuição de probabilidade conjunta dos eventos apresentados na situação hipotética anterior, é correto afirmar que o valor da probabilidade condicional P(R|F) é igual a
Concurso:
PC-RO
Disciplina:
Estatística
Os eventos A1, A2, A3 e A4 formam uma partição do espaço amostral Ω, de tal sorte que
P(Ak) = k/10,
em que k ∈ {1,2,3,4}.
Na situação hipotética apresentada, a probabilidade da intersecção dos eventos complementares de A2, A3 e A4 representada como 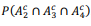 , é igual a
, é igual a
Concurso:
PC-BA
Disciplina:
Estatística
Sobre probabilidade, analise os itens a seguir:
I. Chamamos de espaço amostra, e indicamos por Ω, umconjunto formado por todos os resultados possíveis de umexperimento aleatório. II. Considerando um experimento aleatório, cujo espaço amostralé Ω. Chamaremos de evento todo subconjunto de Ω.
I. Chamamos de espaço amostra, e indicamos por Ω, umconjunto formado por todos os resultados possíveis de umexperimento aleatório. II. Considerando um experimento aleatório, cujo espaço amostralé Ω. Chamaremos de evento todo subconjunto de Ω.
III. Sejam A e B dois eventos, se A ∩ B = ø, A e B sãochamados mutuamente excludentes.
Assinale
Uma caixa contém um número muito grande de lâmpadas, sendo 30% vermelhas,50% azuis e 20% verdes. Qual a probabilidade de, retiradas 3 lâmpadas, serem exatamente uma de cada cor?