Questões de Concurso
Filtrar
270 Questões de concurso encontradas
Página 3 de 54
Questões por página:
Questões por página:
Em uma grande transportadora, sabe-se que a probabilidade deum caminhão partir de um porto no horário marcado é P = (D) = 0,83; a probabilidade de que chegue na hora prevista é P (A) = 0,82; e a probabilidade de que parta e chegue na hora é 78%. Sendo assim, a probabilidade de que o caminhão chegue na hora, dado que partiu na hora, é aproximadamente:
Uma indústria de hardware de computador testará os vícios de um novo chip. Esses vícios se referem a esquentamento ou curto que, embora sejam raros, podem comprometer o funcionamento de computadores novos por completo. A distribuição do número de chips fabricados, por semana, que apresenta esses vícios, é uma distribuição de Poisson com λ = 5. Logo, a probabilidade de que mais de um chip apresente um vício por semana é de, aproximadamente:
Uma pesquisa de opinião sobre três concorrentes cursos de inglês, teve como objetivo avaliar o nível de satisfação com o propósito de lançar um novo curso no mercado. As avaliações de satisfação eram mutuamente excludentes, de modo que os estudantes poderiam avaliar qualquer um dos cursos de forma independente. A escala de satisfação foi definida no intervalo de 1 a 10. Do total de entrevistados,78% avaliaram satisfatoriamente. Desses,50% declararam-se satisfeitos com o primeiro curso,30% satisfeitos com o segundo, e 20% com o terceiro. Sabe-se, ainda, que 5% do total dos entrevistados declararam-se favorável a ambos os cursos. Assim, a percentagem dos entrevistados que se declarara favorável a mais de um dos cursos é:
Sabe-se, com base em dados históricos, que o número de acidentados que chegam em um hospital traumatológico, durante um período de 20 minutos, é distribuído discretamente por uma função modelada por ƒ(x) = e-6 6 x / x!, x ∈ ℕ Assim, a probabilidade de que (no período indicado) mais de quatro acidentados cheguem ao hospital é:
Obs.: Use e −6 ≅ 0,00247875.
Obs.: Use e −6 ≅ 0,00247875.
mostrar texto associado
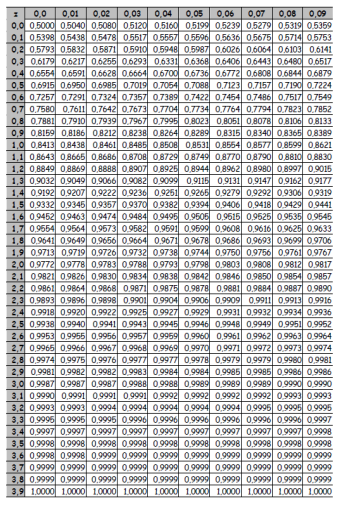
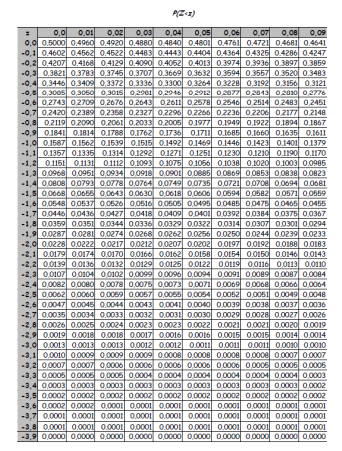
Durante o desenvolvimento de um sistema de controle de qualidade para medição de diâmetros de componentes cilíndricos, um engenheiro modela o erro de fabricação com uma variável aleatória contínua X que segue uma distribuição normal com média μ = 5mm e desvio-padrão σ = 0,02mm. O engenheiro deseja garantir que pelo menos 95% (noventa e cinco por cento) dos componentes produzidos tenham diâmetro dentro da faixa aceitável. Com base nas propriedades da função densidade normal de Gauss, ele define um intervalo simétrico em torno da média μ, de modo que:
P(μ − Zσ ≤ X ≤ μ + zσ) ≥ 0,95
Com base na distribuição normal padrão, o menor valor de z que satisfaz esse critério (e com melhor interpretação) é:
P(μ − Zσ ≤ X ≤ μ + zσ) ≥ 0,95
Com base na distribuição normal padrão, o menor valor de z que satisfaz esse critério (e com melhor interpretação) é: