Questões de Concurso
Filtrar
97 Questões de concurso encontradas
Página 14 de 20
Questões por página:
Em caso de risco iminente a pessoas ou bens, o Corpo de Bombeiros é chamado para cortar e remover árvores. Na escolha de um veículo adequado para remoção de uma árvore, inicialmente, um bombeiro decide realizar uma previsão do peso dessa árvore, a partir do seu volume.
Para estimar o volume dessa árvore, de formato aproximadamente cilíndrico, esse bombeiro decide passar uma corda em volta do seu tronco, para encontrar o comprimento de sua base. Em seguida, mede sua altura, desconsiderando a copa da árvore. Ele encontra 1 metro e 12 metros para o comprimento da base e a altura da árvore, respectivamente. A partir desses dados, ele calcula o volume de um cilindro, cuja base circular e altura são iguais ao comprimento da base e altura da árvore por ele medidos. Ele usa a aproximação 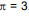 . Finalmente, ele acrescenta 10% a esse cálculo, para corrigir erros de medida.
. Finalmente, ele acrescenta 10% a esse cálculo, para corrigir erros de medida.
A partir desses dados, qual é o volume dessa árvore, a partir da estimativa realizada por esse bombeiro, em metros cúbicos?
A torre de Hanói constitui-se em um jogo estratégico capaz de contribuir no desenvolvimento da memória, no planejamento e na solução de problemas. O jogo se apresenta em uma base que possui três pinos na posição vertical (figura a seguir). No primeiro pino, tem-se uma sequência de discos com ordem crescente de diâmetro, de cima para baixo. O objetivo é passar todos os discos para o último pino com a ajuda do pino central, de modo que no momento da transferência o pino de maior diâmetro nunca fique sobre o de menor diâmetro.
Disponível em:<https://educador.brasilescola.uol.com.br/estrategias-ensino/torre-hanoi.htm> . Acesso em: 10 abr.2018 (Adaptação).
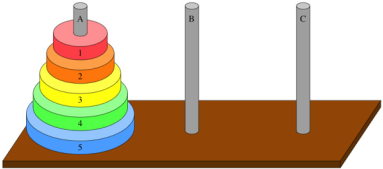
Disponível em: <https://pt.khanacademy.org> . Acesso em: 10 abr.2018.
Considere uma torre de Hanói, em que os discos são constituídos por 5 cilindros retos “furados” de mesma altura,1 centímetro. Sabe-se, também, que os raios desses cilindros estão em progressão aritmética de razão 1 e que o diâmetro dos “furos” de cada disco mede 1 centímetro.
Sabendo-se que o raio do menor disco é de 1 centímetro, qual é o volume ocupado por esses 5 cilindros “furados”, em cm3 ?