Questões de Concurso
Filtrar
97 Questões de concurso encontradas
Página 16 de 20
Questões por página:
Considere que um reservatório possui o formato de um cilindro reto, cujo raio da base mede 4 cm e a altura mede 10 cm. Considere, também, um balde com o formato de um prisma, cuja base é um retângulo com comprimento e largura medindo 2 cm e 1 cm, respectivamente, e cuja altura mede 2 cm.
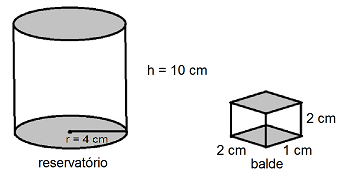
Pretende-se preencher todo o volume desse reservatório com água. Para tal, primeiramente preenche-se o volume do balde com água e, em seguida, despeja-se o conteúdo do balde no reservatório. Esse processo é repetido até que o reservatório esteja totalmente cheio. Dessa forma, a quantidade mínima de vezes que o balde deve ser preenchido com água, para que se preencha todo o volume do reservatório com essa mesma água, será igual a
(considere o valor de π = 3)
Certo combustível preenchia totalmente um reservatório A, na forma de um cilindro circular reto, de raio da base igual a 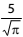 m e altura igual a 5 m. Sabe-se que 4/5 do combustível contido em A foi transferido, sem desperdício, para 10 reservatórios menores B, todos iguais e também cilíndricos, de 1,25 m de altura, preenchendo-os totalmente.
m e altura igual a 5 m. Sabe-se que 4/5 do combustível contido em A foi transferido, sem desperdício, para 10 reservatórios menores B, todos iguais e também cilíndricos, de 1,25 m de altura, preenchendo-os totalmente.
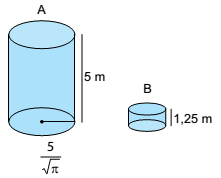
Nessas condições, é correto afirmar que a medida do raio do reservatório B é, em metros, igual
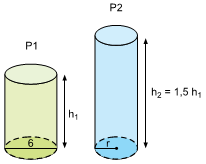
Nessas condições, se a empresa adotar h1 = 10 cm para P1, a medida do raio de P2, em centímetros, deverá ser igual a