Questões de Concurso
Filtrar
152 Questões de concurso encontradas
Página 5 de 31
Questões por página:
Questões por página:
Disciplina:
Física
mostrar texto associado
Suponha‐se que um elevador hidráulico de um posto de gasolina seja acionado mediante um cilindro de área 4.10‐5 m², que o automóvel a ser elevado tenha massa de 2.000 kg e esteja sobre o êmbolo de área 4.10‐3 m² e que a aceleração da gravidade (g) seja igual a 10 m/s². Nesse caso, o deslocamento, que teoricamente deve ter o êmbolo menor, para elevar de 10 cm o automóvel será de 10 m.
Disciplina:
Física
mostrar texto associado
Um fluido pode ser definido como sendo um meio material incapaz de resistir a qualquer valor de tensão de cisalhamento, ou seja, em um fluido em repouso (estático), somente tensões normais podem estar presentes.
Se um bloco tem massa específica de 520 kg/m³ e flutua em um líquido de massa específica 1300 kg/m³. Marque a alternativa que mostra o valor da altura submersa, em centímetro, do bloco se ele tiver 7,5 cm de altura total.
A figura abaixo apresenta um pêndulo, de tamanho L e massa M, preso a um teto. Um disco, de raio r e massa m, é preso na sua extremidade inferior que rotacional em torno de seu próprio eixo.

Calcule o valor do momento de inércia total desse pêndulo.
Represa é uma barreira artificial feita em cursos de rios para a retenção de grandes quantidades de água. Em geral, para fim de cálculos, os engenheiros que trabalham com represas consideram a densidade média da água igual a 1x10³ kg/m³. O campo de atuação da engenharia nessa área é sobretudo direcionado para abastecer de água zonas residenciais, agrícolas e industriais e para a produção de energia elétrica. A imagem abaixo apresenta represa com altura b = 22 m e comprimento a = 600 m.
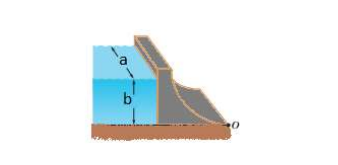
De acordo com o exposto acima, determine qual a força horizontal a que está submetida a represa por causa da pressão manométrica da água. (Se preciso, use g = 10 m/s²).

De acordo com o exposto acima, determine qual a força horizontal a que está submetida a represa por causa da pressão manométrica da água. (Se preciso, use g = 10 m/s²).