Questões de Concurso
Filtrar
1.642 Questões de concurso encontradas
Página 164 de 329
Questões por página:
Questões por página:
Uma câmera de monitoramento está a 12m de uma rodovia que segue em linha reta por um longo trecho. A câmera focaliza um veículo em fuga, como mostra a figura ao lado.
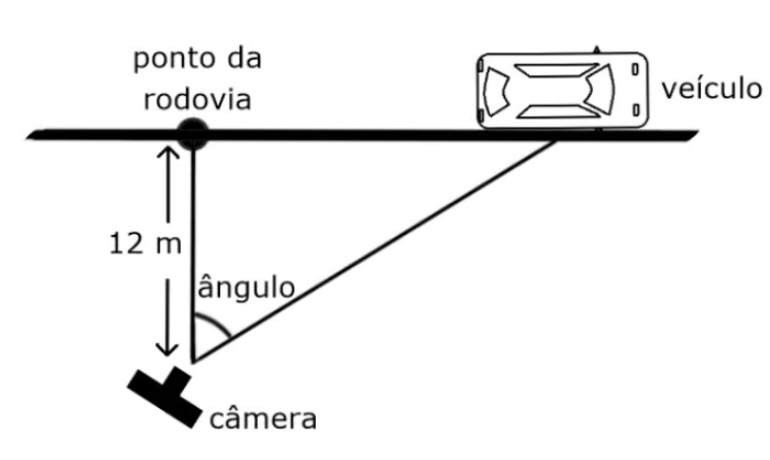
Se o veículo estiver a uma velocidade de 30m/s, quando estiver a 16m do ponto da rodovia mais próximo da câmera, quão rápido deve variar o ângulo da câmera naquele instante para que ela se mantenha apontada para o veículo?
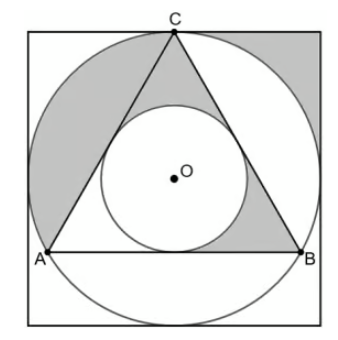
Na figura ao lado, é apresentado o triângulo equilátero ABC e suas circunferências inscrita e circunscrita. Tangenciando a circunferência externa ao triângulo, tem-se o quadrado de lado 10 cm.
De acordo com as informações e a figura ao lado, qual é a área da região sombreada?
Disciplina:
Matemática
A figura a seguir representa o projeto de uma cozinha retangular onde será construída uma despensa, também retangular.
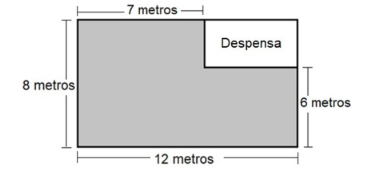
Nesse projeto, a área da despensa, em metros quadrados, corresponde a:

Nesse projeto, a área da despensa, em metros quadrados, corresponde a:
Disciplina:
Matemática
O metro quadrado de um terreno em um loteamento custa R$ 350,00. O terreno é no formato retangular medindo 20 metros de frente (largura) e 30 metros de comprimento. Nestas condições, o valor pago pelo terreno será de
Disciplina:
Matemática
Questão Anulada
Uma esfera de raio igual a 1,0 m, tem um volume igual a
Considere: π = 3