Questões de Concurso

Uma amostra aleatória de tamanho 64 é extraída de uma população de tamanho infinito, normalmente distribuída, média μ e variância conhecida σ². Obtiveram-se com base nos dados desta amostra, além de uma determinada média amostral x,2 intervalos de confiança para μ aos níveis de 95% e 99%, sendo os limites superiores destes intervalos iguais a 20,98 e 21,29, respectivamente. Considerando que na curva normal padrão (Z) as probabilidades P(|Z| > 1,96) = 0,05 e P(|Z| > 2,58) = 0,01, encontra-se que σ² é igual a

Atenção: O enunciado abaixo refere-se à questão.
A porcentagem do orçamento gasto com educação nos municípios de certo estado é uma variável aleatória X com distribuição normal com média μ(%) e variância 4(%)².
Uma amostra aleatória, com reposição, de tamanho n, X₁, X₂, ..., X_n, é selecionada da distribuição de X. Sendo 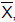a média, amostral dessa amostra, o valor de n para que 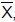não se distancie de sua média por mais do que 0,41% com probabilidade de 96% é igual a

Ao analisar uma amostra aleatória simples composta de 324 elementos, um pesquisador obteve, para os parâmetros média amostral e variância amostral, os valores 175 e 81, respectivamente.

Nesse caso, um intervalo de 95% de confiança de μ é dado por

Para determinado experimento, uma equipe de pesquisadores gerou 20 amostras de tamanho n = 25 de uma distribuição normal, com média µ = 5 e desvio padrão σ = 3. Para cada amostra, foi montado um intervalo de confiança com coeficiente de 0,95 (ou 95%). Com base nessas informações, julgue os itens que se seguem.

I Os intervalos de confiança terão a forma β_i ± 1,176, em que βi é a média da amostra i.

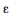
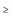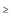II Para todos os intervalos de confiança, β_i + µ β_i - 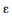, sendo 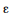a margem de erro do estimador.

III Se o tamanho da amostra fosse maior, mantendo-se fixos os valores do desvio padrão e do nível de confiança, haveria uma redução da margem de erro .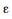

Assinale a opção correta.

Na construção de um intervalo de confiança para a média, conhecida a variância, considerando o intervalo na forma [x + ε; x - ε], sendo x o valor do estimador da média e ε a semi-amplitude do intervalo de confiança ou, como é mais popularmente conhecida, a margem de erro do intervalo de confiança. Considere que, para uma determinada peça automotiva, um lote de 100 peças tenha apresentado espessura média de 4,561 polegada, com desvio padrão de 1,125 polegada. Um intervalo de confiança de 95% para a média apresentou limite superior de 4,7815 e limite inferior de 4,3405. Nessa situação, a margem de erro do intervalo é de, aproximadamente,