Questões de Concurso

Para examinar a opinião de uma população sobre uma proposta, foi montada uma pesquisa de opinião em que foram ouvidas 1680 pessoas, das quais 51,3% se declararam favoráveis à proposta. Os analistas responsáveis determinaram que a margem de erro desse resultado, em um determinado nível de confiança, era de 2 pontos percentuais, para mais ou para menos. Considerando que fosse desejada uma margem de erro de 1 ponto percentual, para mais ou para menos, no mesmo nível de confiança, assinale a alternativa que indique o número de pessoas que deveriam ser ouvidas.

Se Z tem distribuição normal padrão, então:
P(Z < 1,64) = 0,950; P(Z < 2,05) = 0,98; P(Z < 2,24) = 0,987; P(Z < 2,40) = 0,992.

Com o objetivo de se estimar a renda média mensal, µ, em número de salários mínimos (SM) dos servidores públicos com nível de formação superior (bacharéis) de determinada população, selecionou-se uma amostra aleatória de 100 servidores bacharéis. Os resultados obtidos encontram-se na tabela de distribuição de frequências apresentada a seguir: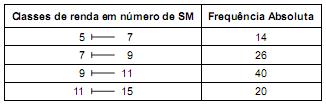



Considere:
I. Que a população de onde a amostra foi retirada é infinita e tem distribuição normal com desvio padrão igual a 1,6 SM.
II. Para a estimativa pontual de µ a média aritmética dos 100 rendimentos apresentados, foi calculada considerando que todos os valores incluídos num intervalo de classe são coincidentes com o ponto médio do intervalo.

Nessas condições, o intervalo de confiança para µ com coeficiente de confiança igual a 96%, baseado nessa amostra, é dado por

Instruções: Para resolver à questão utilize, dentre as informações dadas a seguir, as que julgar apropriadas.

Se Z tem distribuição normal padrão, então:

P(Z < 0,5) = 0,691; P(Z < 1) = 0,841; P(Z < 1,2) = 0,885; P(Z < 1,28) = 0,90.

Com o objetivo de se estimar a idade média, μ, em anos, de ingresso no primeiro emprego formal de jovens de determinada comunidade, selecionou-se uma amostra aleatória de 100 jovens da população de jovens que já haviam ingressado no mercado de trabalho formal. Os resultados obtidos encontram-se na tabela de distribuição de frequências apresentada a seguir:



Considere:

I. Que a população de onde a amostra foi retirada é infinita e tem distribuição normal com desvio padrão igual a 1 ano.

II. Para a estimativa pontual de μ a média aritmética das 100 idades apresentadas, calculada considerando que todos os valores incluídos num intervalo de classe são coincidentes com o ponto médio do intervalo.

Nessas condições, o intervalo de confiança para µ, em anos, com coeficiente de confiança igual a 77%, baseado nessa amostra, é dado por

De uma população infinita X, com distribuição normal, com média µ e variância 9, extraiu-se, aleatoriamente, a seguinte amostra de 4 elementos: {x: 1,2; 3,4; 0,6; 5,6}. Com base no estimador de máxima verossimilhança de µ, para um grau de significância de α, estimou-se o intervalo de confiança para a média em [-0,24; 5,64]. Da mesma população, extraiu-se uma amostra 100 vezes maior que a anterior e verificou-se que, para essa nova amostra, a estimativa da média amostral era igual à obtida com a primeira amostra. Com o mesmo grau de significância α, o intervalo de confiança estimado, com base na nova amostra, foi

Uma pesquisa realizada com 8.400 habitantes de uma cidade, escolhidos aleatoriamente, revelou que 70% deles estavam satisfeitos com o desempenho do prefeito. Considere que é normal a distribuição amostral da frequência relativa dos habitantes satisfeitos com o desempenho do prefeito e que, na curva normal padrão Z, a probabilidade P(Z>1,96) = 0,025. Considerando a cidade com uma população de tamanho infinito, o intervalo de confiança para esta proporção ao nível de confiança de 95%, com base no resultado da amostra, é