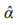Questões de Concurso
Filtrar
141 Questões de concurso encontradas
Página 10 de 29
Questões por página:
Questões por página:
mostrar texto associado
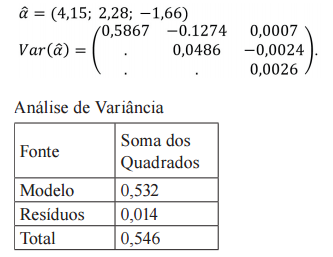
Sobre o procedimento para testar a hipótese H0 : α1 = α2 = 0, pode-se afirmar CORRETAMENTE o seguinte:
mostrar texto associado
O coeficiente de determinação do modelo estimado será aproximadamente:
mostrar texto associado
O pesquisador deseja obter uma estimativa da variação percentual no consumo decorrente do aumento de 1% na renda e da redução de 2% no preço. A variância dessa estimativa é dada por:
Considere duas variáveis aleatórias X e Y. São dados: E [X] = 35, E [Y] = 55, V [X] = 3, V [Y] = 18 e Cov [X, Y] = 5, onde E [ ] indica a média, V [ ] a variância e Cov [, ] a covariância. Assinale a opção que expressa a variância da soma X + Y.
Concurso:
SEDUC
Disciplina:
Estatística
Uma amostra de 10 alunos de uma turma de sexto ano do ensino fundamental teve suas notas de matemática analisadas. Elas foram 7,0 ; 8,0 ; 6,0 ; 7,0 ; 9,5 ; 6,5 ; 7,5 ; 8,0 ; 10,0 e 5,5. A variância dessa distribuição de valores é: