Questões de Concurso
Filtrar
118 Questões de concurso encontradas
Página 16 de 24
Questões por página:
Questões por página:
Concurso:
TRT - 11ª Região (AM e RR)
Disciplina:
Estatística
Suponha que:
I. A variável X, que representa o número mensal de suicídios no país A, tem distribuição de Poisson com média mensal 2. II. A variável Y, que representa o número mensal de suicídios no país B, tem distribuição de Poisson com média mensal 4. III. As variáveis X e Y são independentes.
Nessas condições, a probabilidade de em determinado mês ocorrerem menos de 2 suicídios no país A e exatamente 2 no país B é igual a
Dados: e−1 = 0,37 e−2 = 0,135 e−4 = 0,018
I. A variável X, que representa o número mensal de suicídios no país A, tem distribuição de Poisson com média mensal 2. II. A variável Y, que representa o número mensal de suicídios no país B, tem distribuição de Poisson com média mensal 4. III. As variáveis X e Y são independentes.
Nessas condições, a probabilidade de em determinado mês ocorrerem menos de 2 suicídios no país A e exatamente 2 no país B é igual a
Dados: e−1 = 0,37 e−2 = 0,135 e−4 = 0,018
Concurso:
TRT - 11ª Região (AM e RR)
Disciplina:
Estatística
Um pesquisador está realizando um experimento que consiste em tentativas independentes que podem resultar em sucesso ou fracasso e em que a probabilidade de sucesso é sempre constante. Na tabela de distribuição de frequências a seguir, está registrado o número de tentativas até a obtenção do primeiro sucesso para uma amostra de 100 repetições do experimento:

Seja X a variável aleatória que representa o número de tentativas até a obtenção do primeiro sucesso. Baseado nessa amostra, o valor observado da estatística qui-quadrado apropriado para testar se X se comporta com uma distribuição geométrica de média igual a 5 é dado por

Seja X a variável aleatória que representa o número de tentativas até a obtenção do primeiro sucesso. Baseado nessa amostra, o valor observado da estatística qui-quadrado apropriado para testar se X se comporta com uma distribuição geométrica de média igual a 5 é dado por
Concurso:
TRT - 11ª Região (AM e RR)
Disciplina:
Estatística
Considere as afirmativas abaixo.
I. Se X e Y têm distribuição qui-quadrado com graus de liberdade dados, respectivamente por 2 e 3, então a variável W = (3X/2Y) tem distribuição F (Snedecor) com 2 e 3 graus de liberdade, respectivamente. II. Sendo X uma variável com distribuição normal padrão e Y uma variável com distribuição qui-quadrado com 1 grau de liberdade, então a variável W = (X/√Y ) tem distribuição t de Student com 1 grau de liberdade. III. A distribuição exponencial é um caso particular da distribuição gama. IV. Se X tem distribuição gama com parâmetros a e b, com a ≥ 1 e b > 0, então a variância de X é igual ao produto de a por b.
Está correto o que se afirma em
I. Se X e Y têm distribuição qui-quadrado com graus de liberdade dados, respectivamente por 2 e 3, então a variável W = (3X/2Y) tem distribuição F (Snedecor) com 2 e 3 graus de liberdade, respectivamente. II. Sendo X uma variável com distribuição normal padrão e Y uma variável com distribuição qui-quadrado com 1 grau de liberdade, então a variável W = (X/√Y ) tem distribuição t de Student com 1 grau de liberdade. III. A distribuição exponencial é um caso particular da distribuição gama. IV. Se X tem distribuição gama com parâmetros a e b, com a ≥ 1 e b > 0, então a variância de X é igual ao produto de a por b.
Está correto o que se afirma em
Concurso:
TRT - 11ª Região (AM e RR)
Disciplina:
Estatística
Uma indústria produz lâmpadas do tipo I e II. Considere as seguintes variáveis aleatórias: X = tempo de vida das lâmpadas do tipo I em horas e Y = tempo de vida das lâmpadas do tipo II em horas. De um lote de 500 lâmpadas sendo 200 do tipo I e 300 do tipo II retira-se ao acaso uma lâmpada. Sabe-se que X tem distribuição exponencial com média de 5000 horas e que Y tem distribuição exponencial com média de 8000 horas. Nessas condições, a probabilidade da lâmpada selecionada ter duração entre 4000 e 6000 horas é
Dados: e−0,5 = 0,61 e−0,75 = 0,47 e−0,8 = 0,45 e−1 = 0,37 e−1,2 = 0,30
Dados: e−0,5 = 0,61 e−0,75 = 0,47 e−0,8 = 0,45 e−1 = 0,37 e−1,2 = 0,30
Concurso:
TRT - 11ª Região (AM e RR)
Disciplina:
Estatística
mostrar texto associado
Uma tarefa é realizada pelos funcionários de uma empresa em 3 etapas. O tempo total, de cada funcionário, para a realização da ta- refa é dado pela soma dos tempos de 3 variáveis aleatórias denotadas por Xi, i = 1,2,3, cada uma delas representando o tempo de uma etapa. Sabe-se que o vetor 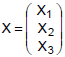 tem distribuição normal multivariada com vetor de médias, dado por
tem distribuição normal multivariada com vetor de médias, dado por 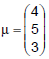 matriz de covariâncias dada por
matriz de covariâncias dada por 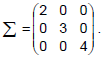 Os dados do vetor μ estão em dias e os da matriz Σ em (dias)². Quatro funcionários são selecionados ao acaso e com reposição dentre todos os funcionários da empresa. Nessas condições, a probabilidade do tempo médio, para a realização da tarefa, desses 4 funcionários ser de pelo menos 15 dias é igual a
Os dados do vetor μ estão em dias e os da matriz Σ em (dias)². Quatro funcionários são selecionados ao acaso e com reposição dentre todos os funcionários da empresa. Nessas condições, a probabilidade do tempo médio, para a realização da tarefa, desses 4 funcionários ser de pelo menos 15 dias é igual a
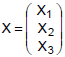 tem distribuição normal multivariada com vetor de médias, dado por
tem distribuição normal multivariada com vetor de médias, dado por 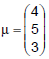 matriz de covariâncias dada por
matriz de covariâncias dada por 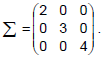 Os dados do vetor μ estão em dias e os da matriz Σ em (dias)². Quatro funcionários são selecionados ao acaso e com reposição dentre todos os funcionários da empresa. Nessas condições, a probabilidade do tempo médio, para a realização da tarefa, desses 4 funcionários ser de pelo menos 15 dias é igual a
Os dados do vetor μ estão em dias e os da matriz Σ em (dias)². Quatro funcionários são selecionados ao acaso e com reposição dentre todos os funcionários da empresa. Nessas condições, a probabilidade do tempo médio, para a realização da tarefa, desses 4 funcionários ser de pelo menos 15 dias é igual a