Questões de Concurso
Filtrar
118 Questões de concurso encontradas
Página 5 de 24
Questões por página:
Questões por página:
Concurso:
EBSERH
Disciplina:
Estatística
Sua consulta médica está marcada para 15h. Você pode tomar um dentre dois caminhos para chegar ao consultório. Pelo primeiro caminho, você demora em média 30 minutos, com desvio padrão de 10 minutos, para chegar ao consultório, segundo uma distribuição normal. Pelo segundo caminho, o tempo médio do trajeto até o consultório é de 25 minutos, com desvio padrão de 5 minutos, também segundo uma distribuição normal. São 14:35. O caminho que tem maior probabilidade de te levar ao consultório no horário marcado é:
Concurso:
TRF - 2ª REGIÃO
Disciplina:
Estatística
Se a variável aleatória X tem distribuição normal com média μ e variância σ2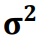
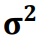, ou seja, X ⁓ N(μ, σ2), s2 = 
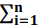(xi–x̄)2/n–1 (variância amostral) é a estimativa de σ2 com base em uma amostra com n observações, [x1, x2, ..., xn]. Assim, a variável T = X – μ/s tem distribuição t de Student com n – 1 graus de liberdade, ou seja, T ~ tn-1. Nesse caso, sabendo que P(T ≤ 2) = 0,968027 e P(T ≥ -2) = 0,031973, é correto afirmar que
Concurso:
TRF - 2ª REGIÃO
Disciplina:
Estatística
ALERT: Essa questão ainda está sendo revisada pela equipe FonteConcursos!
O método dos Mínimos Quadrados Ordinários (MQO) apresenta propriedades estatísticas que o tornam um dos métodos mais populares e eficientes de análise de regressão.
A eficiência desse método depende da validade da seguinte hipótese:
Concurso:
SEDUC-MT
Disciplina:
Estatística
Cinco alunos foram selecionados aleatoriamente e observou-se os seguintes tempos, em minutos, para resolver uma questão de matemática: {15,6,1,12}. Considerando que os tempos seguem uma distribuição exponencial com parâmetro λ, a estimativa de máxima verossimilhança para λ é:
