Filtrar
65 Questões de concurso encontradas
Página 1 de 13
Questões por página:
Questões por página:
Concurso:
Prefeitura de Santo André
Disciplina:
Raciocínio Lógico
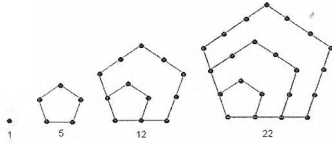
Dentre as representações numéricas, há aquelas que associam um número natural a uma forma geométrica, que quando colocados em ordem crescente de posições (da menor para a maior posição), podemos observar uma estrutura lógica e constante de cálculo para definições quantitativas de uma posição qualquer. É o caso dos chamados de números triangulares, em que sendo o 1º número o 1, os demais são obtidos a partir da estrutura de cálculo [n.(n+1)]/2, onde “ n” é a posição ocupada por este número na sequência em que está inscrito. Com base nessas informações, abaixo fornecemos os primeiros termos da sequência denominada de números pentagonais. Podemos identificar que o 6º termo da sequência, a partir da evolução dos números, será o número:
Em um dado usual de seis faces quadradas, pontuadas de 1 a 6 em cada face, temos que a soma dos pontos das faces opostas é sempre igual a sete. Quatro dados comuns foram empilhados conforme a figura.
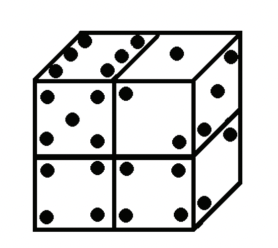
Sabendo que as faces que se confrontam têm pontuação igual, a soma dos pontos das faces ocultas que NÃO se confrontam é igual a

Sabendo que as faces que se confrontam têm pontuação igual, a soma dos pontos das faces ocultas que NÃO se confrontam é igual a
Concurso:
CEFET-MG
Disciplina:
Raciocínio Lógico
Em um dado usual de seis faces quadradas, pontuadas de 1 a 6 em cada face, a soma dos pontos das faces opostas é sempre igual a sete.
Nos dados da figura abaixo,
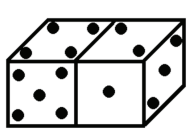
a soma dos pontos das faces que não vemos é igual a
Nos dados da figura abaixo,

a soma dos pontos das faces que não vemos é igual a
Concurso:
CEFET-MG
Disciplina:
Raciocínio Lógico
Em um dado usual de seis faces quadradas, pontuadas de 1 a 6 em cada face, a soma dos pontos das faces opostas é sempre igual a sete.
Nos dados da figura abaixo,
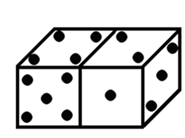
a soma dos pontos das faces que não vemos é igual a
Nos dados da figura abaixo,

a soma dos pontos das faces que não vemos é igual a
Concurso:
CEFET-MG
Disciplina:
Raciocínio Lógico
Os dois quadrados abaixo, quando sobrepostos sem que ocorram cortes ou dobras, formam novas figuras.
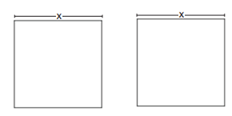
Nesse cenário, uma figura que NÃO pode ser obtida é

Nesse cenário, uma figura que NÃO pode ser obtida é