Questões de Concurso

Considere as n variáveis aleatórias iid, isto é, independentes e identicamente distribuídas X₁, X₂ ,..., X_n com distribuição N(μ,σ²).

Considere ainda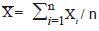
e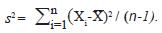

Dessa maneira o quociente entre as variáveis aleatórias independentes 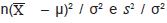é uma variável aleatória:

Se X é uma variável aleatória descrita por uma função conjunto de probabilidades P_X(.), a função de distribuição de probabilidade de X, F(x) terá, entre outras, as seguintes propriedades:

I - F(x) é monotônica não decrescente;
II - lim_x→∞ F(x) = 0 e lim_x→∞ F(x) = 0;
III - F(x) é contínua à direita.

É(São) correta(s) a(s) propriedade(s)

.Sobre variáveis aleatórias, considere as afirmações a seguir.

I - Para toda e qualquer variável aleatória, sua função de densidade de probabilidade fornece a probabilidade de ocorrência de cada valor da variável aleatória considerada, exceto no caso de variáveis aleatórias contínuas, para as quais a probabilidade de ocorrência de um valor específico é zero.

II - A esperança matemática (expectância) de uma variável aleatória discreta, ou seja, seu valor esperado, é a média dessa variável aleatória, que é definida como um navos do somatório dos valores possíveis dessa variável multiplicados por suas respectivas probabilidades.

III - A distribuição binomial é uma extensão direta da Distribuição de Bernoulli, uma vez que o experimento aleatório que caracteriza a binomial nada mais é do que um Experimento de Bernoulli repetido n vezes.

É correto APENAS o que se afirma em

Se X e Y são duas variáveis aleatórias, para as quais são definidas: E(X) e E(Y), suas esperanças matemáticas (expectâncias); Var(X) e Var(Y), suas respectivas variâncias, e Cov(X, Y), a covariância entre X e Y, quaisquer que sejam as distribuições de X e Y, tem-se que