Dados os conjuntos A e B podemos considerar a “união" A ∪ B deles, sua “interseção" A ∩ B e sua “diferença" A − B, definidas da seguinte maneira:
• ( x ∈ A ∪ B) ⇔ (x ∈ A ∨ x ∈ B);
• ( x ∈ A ∩ B) ⇔ (x ∈ A ∧ x ∈ B); e
• ( x ∈ A − B) ⇔ (x ∈ A ∧ x ∉ B)
Um conjunto universo para uma situação é um conjunto U que possui todos os elementos dos conjuntos daquela situação.
Nesta situação-problema temos três conjuntos A, B e C, como na figura
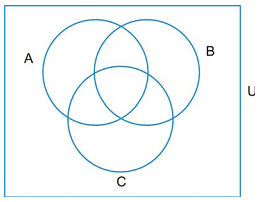
e as seguintes informações sobre eles:
I. U = {1, 2, 3, 4, 5, 6, 7, 8};
II. Os conjuntos A, B e C têm, cada um, 4 (quatro) elementos;
III.1 ∉ A ∪ B ∪ C;
IV.8 ∈ A ∩ B ∩ C;
V. A − B = {2, 5} e B − A = {3, 7};
VI.4 ∉ ( A ∪ B); e
VII. ( A ∩ B) − C = {6}
Assinale a alternativa correta.
• ( x ∈ A ∪ B) ⇔ (x ∈ A ∨ x ∈ B);
• ( x ∈ A ∩ B) ⇔ (x ∈ A ∧ x ∈ B); e
• ( x ∈ A − B) ⇔ (x ∈ A ∧ x ∉ B)
Um conjunto universo para uma situação é um conjunto U que possui todos os elementos dos conjuntos daquela situação.
Nesta situação-problema temos três conjuntos A, B e C, como na figura

e as seguintes informações sobre eles:
I. U = {1, 2, 3, 4, 5, 6, 7, 8};
II. Os conjuntos A, B e C têm, cada um, 4 (quatro) elementos;
III.1 ∉ A ∪ B ∪ C;
IV.8 ∈ A ∩ B ∩ C;
V. A − B = {2, 5} e B − A = {3, 7};
VI.4 ∉ ( A ∪ B); e
VII. ( A ∩ B) − C = {6}
Assinale a alternativa correta.