Concurso:
TRT - 14ª Região (RO e AC)
Disciplina:
Estatística
A função geradora de momentos de uma variável aleatória X é definida como Mx(t) = E[etx] para todos os valores de t na qual a esperança seja finita.
No caso de uma variável aleatória discreta, a função geradora de momentos é definida como: Mx (t) =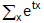 f (x) onde f(x) corresponde à função de probabilidade da variável aleatória X. Tem-se ainda que:
f (x) onde f(x) corresponde à função de probabilidade da variável aleatória X. Tem-se ainda que: 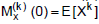 , ou seja, a derivada de ordem k da função geradora de momentos, quando t = 0, gera o momento de ordem k. Considere que uma variável aleatória discreta X tenha uma função geradora de momentos igual a: Mx (t) = 1/6 (et + e2t + e3t + e4t + e5t + e6t). Os valores da média e variância de X são, respectivamente:
, ou seja, a derivada de ordem k da função geradora de momentos, quando t = 0, gera o momento de ordem k. Considere que uma variável aleatória discreta X tenha uma função geradora de momentos igual a: Mx (t) = 1/6 (et + e2t + e3t + e4t + e5t + e6t). Os valores da média e variância de X são, respectivamente:
No caso de uma variável aleatória discreta, a função geradora de momentos é definida como: Mx (t) =
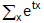 f (x) onde f(x) corresponde à função de probabilidade da variável aleatória X. Tem-se ainda que:
f (x) onde f(x) corresponde à função de probabilidade da variável aleatória X. Tem-se ainda que: 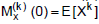 , ou seja, a derivada de ordem k da função geradora de momentos, quando t = 0, gera o momento de ordem k. Considere que uma variável aleatória discreta X tenha uma função geradora de momentos igual a: Mx (t) = 1/6 (et + e2t + e3t + e4t + e5t + e6t). Os valores da média e variância de X são, respectivamente:
, ou seja, a derivada de ordem k da função geradora de momentos, quando t = 0, gera o momento de ordem k. Considere que uma variável aleatória discreta X tenha uma função geradora de momentos igual a: Mx (t) = 1/6 (et + e2t + e3t + e4t + e5t + e6t). Os valores da média e variância de X são, respectivamente: