Em uma população finita de tamanho N, onde existem k indivíduos com uma característica de interesse, ao se selecionar uma amostra aleatória de tamanho n sem reposição, o número de indivíduos com a característica na amostra (R) é uma variável aleatória com distribuição hipergeométrica. A probabilidade de se ter exatamente r indivíduos na amostra com a característica de interesse é dada por

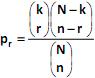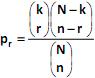, onde max (0, n – N + k) = r = min (k, n).

Analise.

I. Para N = 100, k = 20, n = 10 e r = 3, E(R) = 2 e Var(R) = 144/99.

II. Para N = 100, k = 20, n = 5 e r = 3, E(R) = 1 e Var(R) = 8/10.

III. Para N = 10000, k = 2000, n = 100 e r = 3, E(R) = 20 e Var(R) = 15,84.

IV. Para N = 10000, k = 1000, n = 100 e r = 3, E(R) = 10 e Var(R) ˜ 9.

V. Para N = 10000, k = 2000, n = 10 e r = 0, P(R = 0) ˜ 0,1074.

Estão corretas apenas as alternativas