Questões de Concurso

Uma variável aleatória X representa o número de contribuintes que chega a cada hora para ser atendido em um órgão público. Supõe-se que X tem distribuição de Poisson, com parâmetro λ, ou seja, 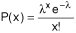, sendo e a base do logaritmo (ln) tal que ln(e) = 1. Se P(x = 2) = P(x = 3), então a probabilidade de que menos de 3 contribuintes cheguem em 1 hora é

Dados:

e^-1 = 0,37,

e^-2 = 0,14 e

e^-3 = 0,05

Considere a distribuição dos salários, em R$ 1.000,00, dos funcionários lotados em uma repartição pública, representada abaixo pela tabela de frequências relativas acumuladas, sendo k a frequência relativa acumulada do 4° intervalo de classe.

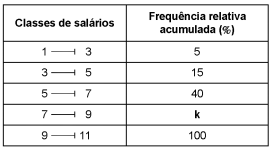
Sabe-se que a média aritmética (Me) foi calculada considerando que todos os valores incluídos num certo intervalo de classe são coincidentes com o ponto médio desse intervalo, que a mediana (Md) foi calculada pelo método da interpolação linear e que a moda (Mo) foi obtida pela relação de Pearson, ou seja, Mo = 3Md - 2Me. Dado que Me = R$ 7.200,00, então Mo é igual a

Para obter um intervalo de confiança de 90% para a média p de uma população normalmente distribuída, de tamanho infinito e variância desconhecida, extraiu-se uma amostra aleatória de tamanho 9 dessa população, obtendo-se uma média amostral igual a 15 e variância igual a 16. Considerou-se a distribuição t de Student para o teste unicaudal tal que a probabilidade P(t - t0 os) = 0,05, com n graus de liberdade. Com base nos dados da amostra, esse intervalo é igual a