Questões de Concurso
Filtrar
3.606 Questões de concurso encontradas
Página 306 de 722
Questões por página:
Questões por página:
Concurso:
INFRAERO
Disciplina:
Estatística
Seja a variável aleatória contínua X com função densidade de probabilidade dada por: 
Nessas condições, o valor de K deve ser
Concurso:
INFRAERO
Disciplina:
Estatística
Seja a variável aleatória bidimensional (X, Y) com função de probabilidade dada por: 
A variância da variável aleatória Z = X + Y é dada por
Concurso:
INFRAERO
Disciplina:
Estatística
Atenção: Para resolver a questão de número 48, dentre as informações dadas abaixo, utilize aquela que julgar apropriada:
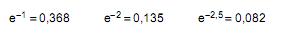
O número de passageiros que chegam a um posto de atendimento de uma empresa de aviação para fazer o check-in às quartas-feiras pela manhã tem distribuição de Poisson com taxa média de 5 passageiros por minuto. A probabilidade de chegar a esse mesmo posto, numa quarta-feira pela manhã, pelo menos 2 passageiros em 30 segundos, é de
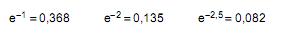
O número de passageiros que chegam a um posto de atendimento de uma empresa de aviação para fazer o check-in às quartas-feiras pela manhã tem distribuição de Poisson com taxa média de 5 passageiros por minuto. A probabilidade de chegar a esse mesmo posto, numa quarta-feira pela manhã, pelo menos 2 passageiros em 30 segundos, é de
Concurso:
INFRAERO
Disciplina:
Estatística
Um analista de mercados está coletando informações sobre a variável X = preço de determinado produto. Ele coletou uma amostra aleatória, sem reposição, de tamanho n de uma população de 45 compradores do produto. Sabendo-se que a variância da média amostral (X) dos preços pagos pelos n clientes pelo produto é 1/11 da variância populacional (variância de X para a população finita de 45 compradores), o valor de n é
Concurso:
INFRAERO
Disciplina:
Estatística
Um dado é viciado de tal modo que a probabilidade de ocorrer face par é duas vezes mais provável do que ocorrer face ímpar. O dado é lançado duas vezes independentemente. Considere os seguintes eventos:
A = a soma dos pontos das faces é 6;
B = o número da face do primeiro dado é menor do que 3.
Nessas condições, a probabilidade de A, sabendo que ocorreu B, é
A = a soma dos pontos das faces é 6;
B = o número da face do primeiro dado é menor do que 3.
Nessas condições, a probabilidade de A, sabendo que ocorreu B, é