Questões de Concurso
Filtrar
3.606 Questões de concurso encontradas
Página 31 de 722
Questões por página:
2 3 1 4 2 2 1 2 3 4
3 2 1 5 3 2 1 5 3 2
O maior número de vítimas de acidentes de trânsito que dão entrada no pronto-socorro em 25% dos dias mais calmos é:
A Tabela 1 deve ser utilizada na solução da questão.
Tabela da distribuição normal padronizada – P(0≤Z≤z)
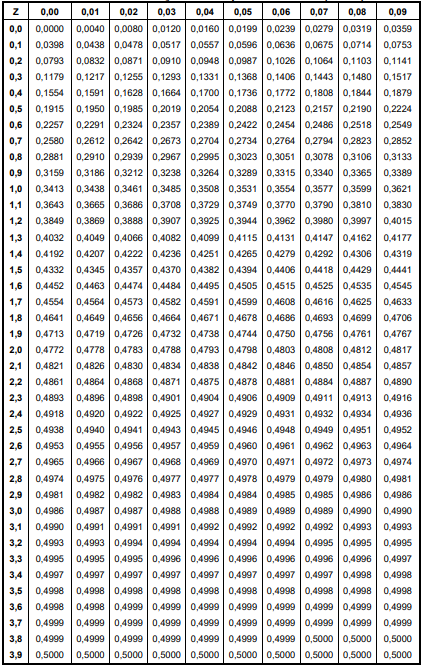
Tabela 1 Fonte: Stevenson, W.J.1986. Estatística aplicada à administração. São Paulo, Harbra, p.461
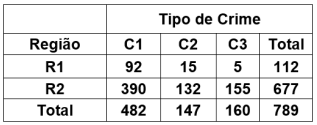
Um estudo tem o objetivo de verificar se existe independência entre tipos de crimes e regiões de um país. A seguinte Tabela de Contingência mostra os números observados em uma amostra aleatória de tamanho n = 789 casos registrados nas regiões.
Sabe-se que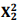 
= 27,91 e P( 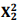> 27,91) = 0,0000. Então, é correto afirmar que as frequências esperadas das células (C1, R2) e (C3, R1), o valor-p e a decisão quanto à relação entre Tipo de Crime e Região, do teste da hipótese de independência entre Tipo de Crime e Região, serão:
Supondo que [X1, X2, ..., Xn] seja uma amostra aleatória da variável aleatória X com distribuição Poisson
com parâmetro θ, ou seja, P(θ), é correto afirmar que
A forma geral de representar uma classe de séries temporais não estacionárias é o modelo utorregressivo integrado médias móveis de ordem (p, d, q), ou seja, ARIMA(p, d, q), em que p é o grau do polinômio aracterístico da parte autorregressiva Φ(B), q é o grau do polinômio característico da parte média móveis θ(B) e d é o grau de diferenciação ▽d, ou seja, Φ(B)▽dZt = θ(B)at em que ⊽dZt = ωt. Desse modo, tem-se Φ(B)ωt = θ(B)at que é um modelo ARMA(p, q).
A uma determinada série temporal, ajustou-se um modelo da classe ARIMA(p, d, q), e os resultados do ajuste estão expostos a seguir:
Modelo ARIMA ajustado à série temporal
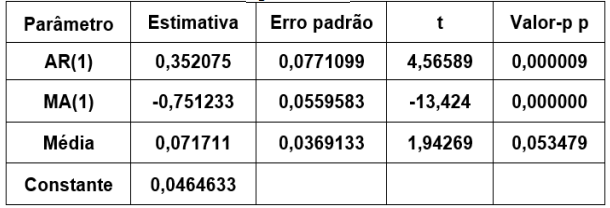
Então, é correto afirmar, com aproximação de três (03) casas decimais, que
