Questões de Concurso
Filtrar
3.606 Questões de concurso encontradas
Página 313 de 722
Questões por página:
Considere X e Y duas variáveis aleatórias quaisquer e as afirmativas abaixo:
I. Se Z = 8X + 9Y, então VAR(Z) = 8VAR(X) + 9VAR(Y) + 2 COV(X, Y).
II. Se W = 8X + 9Y + 10, então E(W) = 8E(X) + 9E(Y) + 10.
III. Se COV(X, Y) = 0, então X e Y são independentes.
É correto afirmar que:
Considere os dois modelos de regressão linear simples:
Yi = ß0 ß1 Xi + µi e Zi = a0 + a1 Wi + vi, onde µi e vi são as variáveis residuais e a0, a1, ß0, ß1, os respectivos parâmetros. O segundo modelo se diferencia do primeiro por suas variáveis Zi e Wi apresentarem escalas diferentes de Yi e Xi . (Zi = aYi e Wi = bXi, com a e b constantes positivas).
Das afirmativas abaixo:
I. Os estimadores de mínimos quadrados (ordinários) a0 e a1 são iguais aos de ß0 e ß1.
II. A variância estimada de vi é a2 vezes a variância estimada de µi.
III. Os coeficientes de determinação dos dois modelos são iguais.
É correto afirmar que:
A tabela abaixo mostra o número de boletim de ocorrência por dia, durante 30 dias, em certa delegacia. A porcentagem de dias em que teve 8 ou mais boletins de ocorrência por dia é:
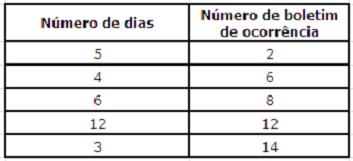
Uma pesquisa realizada em uma escola X mostrou o uso do facebook entre os alunos com diferentes faixas etárias, conforme mostra a tabela abaixo. A moda é igual a:
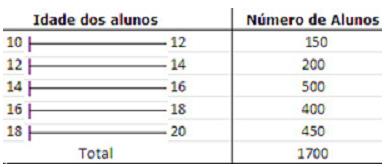
A tabela abaixo mostra a taxa de fertilidade no período de 2000 a 2005.A mediana da taxa de fertilidade é:
