Questões de Concurso
Filtrar
3.606 Questões de concurso encontradas
Página 452 de 722
Questões por página:
Questões por página:
Concurso:
INSS
Disciplina:
Estatística
mostrar texto associado
Com base nas informações apresentadas no texto acima, julgue o item que se segue.
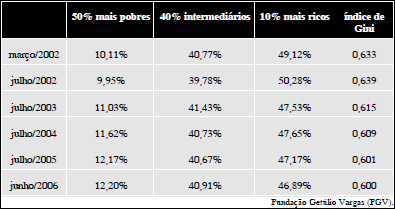
A renda média dos trabalhadores em 2006 foi superior a R$ 350,00.
A renda média dos trabalhadores em 2006 foi superior a R$ 350,00.
Concurso:
INSS
Disciplina:
Estatística
mostrar texto associado
Com base nas informações apresentadas no texto acima, julgue o item que se segue.
O índice de Gini é uma razão sobre a curva de Lorenz que mede o grau de assimetria na distribuição de renda da população. Esse índice varia de zero a infinito, e quanto mais próximo de zero estiver o índice, menor será o grau de assimetria da distribuição de renda dos trabalhadores.
O índice de Gini é uma razão sobre a curva de Lorenz que mede o grau de assimetria na distribuição de renda da população. Esse índice varia de zero a infinito, e quanto mais próximo de zero estiver o índice, menor será o grau de assimetria da distribuição de renda dos trabalhadores.
Concurso:
INSS
Disciplina:
Estatística
mostrar texto associado
Com base nas informações apresentadas no texto acima, julgue o item que se segue.
Em 2006, estima-se pela desigualdade de Markov que o primeiro quartil da distribuição de renda dos trabalhadores seja inferior a R$ 160,00.
Em 2006, estima-se pela desigualdade de Markov que o primeiro quartil da distribuição de renda dos trabalhadores seja inferior a R$ 160,00.
Concurso:
INSS
Disciplina:
Estatística
Para a realização de um estudo, 400 trabalhadores serão selecionados aleatoriamente de uma população de N trabalhadores. De acordo com as informações prestadas, cada trabalhador será classificado como A ou B. Haverá XA pessoas classificadas como A e XB pessoas classificadas como B, de modo que XA + XB = 400. A probabilidade de uma pessoa ser classificada como A é 0 PAB é 0 PB
Considere que xt= (XA, XB) seja um vetor aleatório transposto. Nesse caso, os autovalores da matriz de covariância de x são iguais a 800 × PA × PBe 0, e os respectivos autovetores são 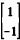 e
e 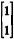 .
.
Concurso:
INSS
Disciplina:
Estatística
Para a realização de um estudo, 400 trabalhadores serão selecionados aleatoriamente de uma população de N trabalhadores. De acordo com as informações prestadas, cada trabalhador será classificado como A ou B. Haverá XA pessoas classificadas como A e XB pessoas classificadas como B, de modo que XA + XB = 400. A probabilidade de uma pessoa ser classificada como A é 0 < PA < 1, enquanto a probabilidade de uma pessoa ser classificada como B é 0 < PB < 1. Com base nessas informações, julgue o item subseqüente.
As variáveis XA e XB são positivamente correlacionadas, e a correlação é superior a 0,5.
As variáveis XA e XB são positivamente correlacionadas, e a correlação é superior a 0,5.