80 Questões de concurso encontradas
Página 3 de 16
Questões por página:
Considere a equação de regressão Yi = α + β. Xi + εi onde Y e X são as variáveis explicada e explicativa, respectivamente, ε é o erro aleatório e α e β os parâmetros a estimar. São supostos válidos todos os pressupostos clássicos do Modelo de Regressão Linear Simples (MRLS). Além disso, para determinada amostra de pares (X, Y), foram calculadas as estatísticas p ( X, Y ) = 0,8, 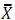 = 6 . ,
= 6 . ,  = 15, DP (Y ) = 5 e DP ( X ) = 2 . Portanto, a partir do método de Mínimos Quadrados Ordinários os estimadores de α e β são
= 15, DP (Y ) = 5 e DP ( X ) = 2 . Portanto, a partir do método de Mínimos Quadrados Ordinários os estimadores de α e β são
Suponha que para a realização de um teste de hipóteses sobre determinado parâmetro estão disponíveis duas alternativas. Na tabela abaixo são apresentadas as probabilidades de rejeição da hipótese nula quando ela é falsa.
Então, pode-se afirmar que
Suponha que o número semanal de pessoas que recorrem a Defensoria Pública em casos que requerem de Mandados de Segurança (MS) segue uma variável aleatória de Poisson com parâmetro λ = 16. Nas últimas 25 semanas o número médio de registros foi de 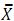 = 15. Usando o Teorema do Limite Central, com Ø( - 1,75 ) = 4 % , sendo Ø( .) é a distribuição acumulada da Normal Padrão, pode-se afirmar que a estimativa para o intervalo de confiança que conteria o verdadeiro valor de λ com 92% de probabilidade é
= 15. Usando o Teorema do Limite Central, com Ø( - 1,75 ) = 4 % , sendo Ø( .) é a distribuição acumulada da Normal Padrão, pode-se afirmar que a estimativa para o intervalo de confiança que conteria o verdadeiro valor de λ com 92% de probabilidade é