Questões da prova:
FAFIPA - 2025 - Prefeitura de Araucária - PR - Auditor Fiscal do Município
limpar filtros
50 Questões de concurso encontradas
Página 8 de 10
Questões por página:
Questões por página:
Concurso:
Prefeitura de Araucária - PR
Disciplina:
Matemática
Em um polígono convexo, a quantidade de diagonais D e a soma dos ângulos internos S podem ser calculas pelas seguintes fórmulas:
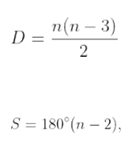
onde n é o número de lados do polígono.
Sabe-se também que um polígono convexo é regular quando todos os seus lados e ângulos internos são congruentes. Sabendo disso, assinale a alternativa que contém a informação CORRETA sobre um polígono regular.
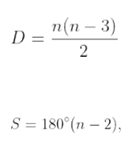
onde n é o número de lados do polígono.
Sabe-se também que um polígono convexo é regular quando todos os seus lados e ângulos internos são congruentes. Sabendo disso, assinale a alternativa que contém a informação CORRETA sobre um polígono regular.
Concurso:
Prefeitura de Araucária - PR
Disciplina:
Matemática
Em um jogo de caça-níqueis, o rolo tem três posições, e cada uma pode ser preenchida com uma das seguintes frutas: limão, cereja ou maçã. Ou seja, em cada uma das posições o jogador pode obter uma das três frutas.
No exemplo da figura, a última fruta ainda está sendo sorteada.
De todas as combinações possíveis, em qual percentual as três frutas serão iguais (ou seja, todas as frutas nas três posições serão a mesma)?

No exemplo da figura, a última fruta ainda está sendo sorteada.
De todas as combinações possíveis, em qual percentual as três frutas serão iguais (ou seja, todas as frutas nas três posições serão a mesma)?
Concurso:
Prefeitura de Araucária - PR
Disciplina:
Raciocínio Lógico
Questão Anulada
Em um museu, foram realizadas exposições com diferentes temas, e alguns quadros foram classificados em três categorias: Nordeste, Bahia e Arte Moderna. Durante a exposição, foram apresentados os seguintes dados:
-32 quadros faziam parte do tema Nordeste, sendo que 12 deles faziam parte também do tema Bahia.
-20 quadros faziam parte do tema Arte Moderna.
-6 quadros pertenciam simultaneamente às categorias Nordeste e Arte Moderna.
-4 quadros pertenciam simultaneamente às categorias Bahia e Arte Moderna.
-Apenas 2 quadros pertenciam a todas as três categorias.
Com base nessas informações, quantos quadros no total pertencem a pelo menos uma dessas três categorias?
-32 quadros faziam parte do tema Nordeste, sendo que 12 deles faziam parte também do tema Bahia.
-20 quadros faziam parte do tema Arte Moderna.
-6 quadros pertenciam simultaneamente às categorias Nordeste e Arte Moderna.
-4 quadros pertenciam simultaneamente às categorias Bahia e Arte Moderna.
-Apenas 2 quadros pertenciam a todas as três categorias.
Com base nessas informações, quantos quadros no total pertencem a pelo menos uma dessas três categorias?
Concurso:
Prefeitura de Araucária - PR
Disciplina:
Raciocínio Lógico
A tabela-verdade a seguir apresenta algumas proposições com valores lógicos ocultos, representados pelas letras a, b e c:
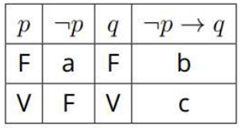
Com base nas regras lógicas e na análise da tabela, determine o valor lógico correspondente a a, b e c, respectivamente.

Com base nas regras lógicas e na análise da tabela, determine o valor lógico correspondente a a, b e c, respectivamente.
Concurso:
Prefeitura de Araucária - PR
Disciplina:
Matemática
O texto seguinte servirá de base para responder à questão.
Divisibilidade
Considere dois números inteiros positivos a e b. Dizemos que a é divisível por b quando a divisão de a por b resulta em um quociente inteiro, ou seja, quando o resto dessa divisão é igual a zero.
Em termos matemáticos, escrevemos isso como a ÷ b = q, onde q é um número inteiro e o resto é zero.
Por exemplo:
• O número 15 é divisível por 5 porque 15 ÷ 5 = 3 e o resto é zero.
•Da mesma forma,15 também é divisível por 3, já que 15 ÷ 3 = 5 e novamente o resto é zero.
No entanto, se tentarmos dividir 15 unidades igualmente entre 2 pessoas, cada pessoa receberá 7, e sobrará uma unidade. Isso acontece porque a divisão tem resto 1, o que significa que 15 não é divisível por 2.
Assim, concluímos que:
• 15 é divisível por 5 e por 3, mas não é divisível por 2.
Considere as seguintes afirmações sobre divisibilidade:
-Se um número é divisível por 4, então ele também é divisível por 2.
-Um número n é divisível por 12 se, e somente se, n é divisível por 4 e por 3.
-Se n é divisível por 6, então n é divisível por 3.
Com base nessas informações, analise as proposições e assinale a alternativa CORRETA.
Divisibilidade
Considere dois números inteiros positivos a e b. Dizemos que a é divisível por b quando a divisão de a por b resulta em um quociente inteiro, ou seja, quando o resto dessa divisão é igual a zero.
Em termos matemáticos, escrevemos isso como a ÷ b = q, onde q é um número inteiro e o resto é zero.
Por exemplo:
• O número 15 é divisível por 5 porque 15 ÷ 5 = 3 e o resto é zero.
•Da mesma forma,15 também é divisível por 3, já que 15 ÷ 3 = 5 e novamente o resto é zero.
No entanto, se tentarmos dividir 15 unidades igualmente entre 2 pessoas, cada pessoa receberá 7, e sobrará uma unidade. Isso acontece porque a divisão tem resto 1, o que significa que 15 não é divisível por 2.
Assim, concluímos que:
• 15 é divisível por 5 e por 3, mas não é divisível por 2.
Considere as seguintes afirmações sobre divisibilidade:
-Se um número é divisível por 4, então ele também é divisível por 2.
-Um número n é divisível por 12 se, e somente se, n é divisível por 4 e por 3.
-Se n é divisível por 6, então n é divisível por 3.
Com base nessas informações, analise as proposições e assinale a alternativa CORRETA.