Questões da prova:
IFPI - 2022 - Instituto Federal de Educação, Ciência e Tecnologia do Piauí (IFPI) - Professor - Matemática
limpar filtros
60 Questões de concurso encontradas
Página 1 de 12
Questões por página:
Questões por página:
Disciplina:
Matemática
Considerando que 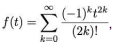 a alternativa correta que contém, respectivamente,
a alternativa correta que contém, respectivamente, 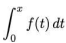 e raio de convergência de f(t) é:
e raio de convergência de f(t) é:
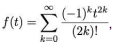 a alternativa correta que contém, respectivamente,
a alternativa correta que contém, respectivamente, 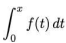 e raio de convergência de f(t) é:
e raio de convergência de f(t) é:
Disciplina:
Matemática
Seja a série de potências representada por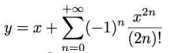 o valor da expressão
o valor da expressão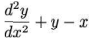 é igual a:
é igual a:
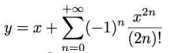 o valor da expressão
o valor da expressão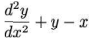 é igual a:
é igual a:
Disciplina:
Matemática
Uma solução para a integral indefinida 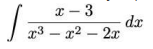 está na alternativa:
está na alternativa:
Disciplina:
Matemática
Calculando o valor da integral definida, a seguir,  obtemos o resultado que está na alternativa:
obtemos o resultado que está na alternativa:
 obtemos o resultado que está na alternativa:
obtemos o resultado que está na alternativa:
Disciplina:
Matemática
O valor do limite 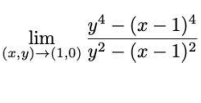 é igual a:
é igual a: