Questões de Concurso
Filtrar
3.619 Questões de concurso encontradas
Página 360 de 724
Questões por página:
Questões por página:
Uma variável aleatória X tem distribuição normal com média 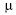 e desvio padrão
e desvio padrão 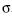 . Desejando-se fazer um teste de hipóteses para a média de X do tipo,
. Desejando-se fazer um teste de hipóteses para a média de X do tipo, 
com base numa amostra de 100 observações, a região crítica apropriada ao teste, dada em termos da média amostral 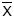 , para que a probabilidade de se cometer erro do tipo I seja a metade da de se cometer erro do tipo II, é dada por
, para que a probabilidade de se cometer erro do tipo I seja a metade da de se cometer erro do tipo II, é dada por
A amostra 0,3; 1,2; 1,1; 0,9; 0,8; 0,5; procede de uma população com função densidade f(x) = 1/θ, 0 < x < θ. Os estimadores de máxima verossimilhança da média e da variância da população são, respectivamente,
A análise fatorial tem como objetivo principal descrever a variabilidade original de um vetor aleatório X com m componentes
Assinale a alternativa correta.
Se retirarmos uma amostra aleatória de 1200 observações de uma população com distribuição uniforme no intervalo [17, 29], a distribuição da média amostral 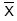 será, aproximadamente,
será, aproximadamente,