Questões de Concurso

Para estimar o valor médio das indenizações por danos morais, ordenadas por um determinado juízo, realiza-se, no âmbito da vara, uma amostra aleatória simples de tamanho n = 16. Nesta a média amostral apurada foi de R$ 7.000. A variância já era conhecida de outros levantamentos, sendo igual a 160.000. Logo, usando o TLC e considerando a normal-padrão Z tal que

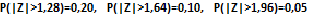
O intervalo de confiança para a média das indenizações, com 90% de probabilidade, é:

Para estimar a média populacional μ é sugerido o estimador 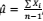onde Xi é o indivíduo de ordem i de uma amostra aleatória simples extraída daquela população. Então, é correto afirmar que:

Seja X1, X2, X3....., ...., X25 um conjunto de variáveis aleatórias que representa o número de processos autuados por dia nas 25 varas que compõem um tribunal, todas identicamente distribuídas com média 15 e variância 16. Adicionalmente, são dadas as seguintes informações sobre a normal-padrão:

P(|Z|>1,25)=0,21, P(|Z|>1,50)=0,13, P(|Z|>1,75)=0,08