2. Questões de Concurso

Filtrar

Questões por página:

O diagrama de ramo e folhas abaixo corresponde às observações das idades de 50 pacientes escolhidos em um determinado bairro de uma cidade:


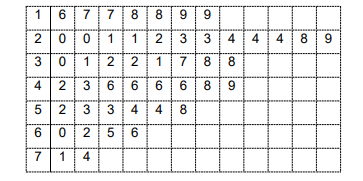
Imagem associada para resolução da questão

Assinale a alternativa que apresenta o valor do módulo da diferença entre a mediana e a moda destas idades observadas.

Assinale a alternativa incorreta.

Considere a seguinte tabela de contingência, em que são obtidas informações de dois exames para detectar um determinado tipo de doença coronária: um padrão ouro e outro teste.


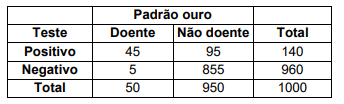
Imagem associada para resolução da questão

Analise as afirmativas a seguir e dê valores Verdadeiro (V) ou Falso (F).
( ) O teste apresenta Sensibilidade e especificidade de 90%. ( ) O teste apresenta Valor preditivo positivo de 50%. ( ) O teste apresenta Valor preditivo negativo de 80%.

Assinale a alternativa que apresenta a sequência correta de cima para baixo.


Para obter resultados precisos do ajuste de modelo, alguns modelos matemáticos podem ser usados na análise de séries temporais, entre os quais não se inclui o modelo ______.
Assinale a alternativa correta que preencha corretamente a lacuna.
Considere o processo estocástico de média móvel MA(1) escrito da forma:
Xt = θ0 + εt + θ1εt-1 para t = 1,2,3, ... ..
em que εt é uma sequência de variáveis aleatórias independentes e identicamente distribuídas com média 0 e variância σ2.
Assinale a alternativa que apresenta respectivamente a média e a variância de Xt .
© 2016-2025 Fonte Concursos - Questões de Concurso e Plano de Estudo