Questões de Concurso
Filtrar
3.537 Questões de concurso encontradas
Página 594 de 708
Questões por página:
Questões por página:
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
A amostra aleatória { X1, X2, X3, ... , X9 } foi extraída de uma população normal de tamanho infinito com variância (σ2) desconhecida.
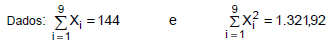
Com base nesta amostra, deseja-se obter um intervalo de confiança de 90% para a média μ da população utilizando a distribuição t de Student levando em conta a tabela a seguir.
Este intervalo é igual a
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
Uma amostra aleatória de tamanho 225 é extraída de uma população (P1) normalmente distribuída e de tamanho infinito. Sabe-se que a variância de P1 é igual a 64. Com base nesta amostra, um intervalo de confiança de nível (1 − α) foi construído para a média μ' de P1 e foi igual a [28,64 ; 31,36]. Em uma outra população (P2), independente da primeira, também normalmente distribuída e de tamanho infinito com média μ'', obteve-se com base em uma amostra aleatória de tamanho 400 um intervalo de confiança de nível (1 − α) para μ'' igual a [20,286 ; 21,714]. O desvio populacional de P2 é igual a
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
Seja X uma variável aleatória uniformemente distribuída no intervalo (m , n) em que m e n são desconhecidos. Utiliza-se o método dos momentos para encontrar os estimadores para m e n (mˆ e nˆ , respectivamente). De uma amostra aleatória da respectiva população de tamanho 8, obteve-se uma média amostral igual a 6 e o momento de segunda ordem igual a 37,6875.
Com base nos resultados desta amostra, encontra-se que o resultado da divisão de mˆ por nˆ apresenta um valor igual a
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
Em um laboratório é realizada uma série de 40 experiências, consistindo em 4 provas cada uma. Em cada experiência foi anotado o número de sucessos (x) atingido e o quadro abaixo apresenta o resultado final.
Dado que o número de sucessos em cada experiência obedece a uma distribuição binomial, ou seja,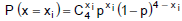 
, obtém-se pelo método da verossimilhança, com base nos dados apresentados pelo quadro, que a estimativa pontual p* do parâmetro
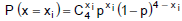, obtém-se pelo método da verossimilhança, com base nos dados apresentados pelo quadro, que a estimativa pontual p* do parâmetro p é tal que
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
Uma amostra aleatória (X , Y) é extraída, com reposição, de uma população normalmente distribuída com média μ e variância σ2 diferente de zero. Deseja-se obter uma estimativa de μ com a utilização da classe de estimadores não viesados E = 2mX + nY, sendo m e n parâmetros reais. Dentre todos os estimadores determinados por esta classe é escolhido aquele que é o mais eficiente. Isto significa que o valor de m é igual a
