Questões de Concurso
Filtrar
3.619 Questões de concurso encontradas
Página 669 de 724
Questões por página:
Questões por página:
Concurso:
TRT - 17ª Região (ES)
Disciplina:
Estatística
mostrar texto associado
O desvio médio absoluto, definido por 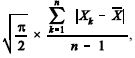 é uma estatística não-tendenciosa para o desvio padrão d.
é uma estatística não-tendenciosa para o desvio padrão d.
Concurso:
TRT - 17ª Região (ES)
Disciplina:
Estatística
mostrar texto associado
A função 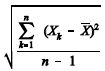 é um estimador tendencioso para o desvio padrão d.
é um estimador tendencioso para o desvio padrão d.
Concurso:
TRT - 17ª Região (ES)
Disciplina:
Estatística
mostrar texto associado
A soma ![]() é uma estatística suficiente e completa para a estimação dos parâmetros m e d.
é uma estatística suficiente e completa para a estimação dos parâmetros m e d.
Concurso:
TRT - 17ª Região (ES)
Disciplina:
Estatística
Concurso:
TRT - 17ª Região (ES)
Disciplina:
Estatística
mostrar texto associado
Assintoticamente, a distribuição da mediana amostral é normal, com média m e desvio padrão maior que ![]()
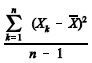 é o estimador de máxima verossimilhança para d2.
é o estimador de máxima verossimilhança para d2.