2. Questões de Concurso

Filtrar

Questões por página:
mostrar texto associado
O tempo de vida dos motores de automóveis de certo tipo fabricados pela Indústria A pode ser considerado uma variável aleatória com distribuição normal com média 250.000 km e desvio padrão de 20.000 km. Suponha que a fábrica A estabeleça uma garantia de x (km) e se propõe a substituir todo motor que tenha tempo de vida inferior a x. O valor de x, em km, para que a porcentagem de motores substituídos seja, no máximo, de 0,1% é igual a

A função geratriz de momentos da variável aleatória contínua X é dada por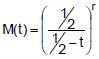 , para t < ½ e onde r é parâmetro de X.

O valor de r para que X tenha distribuição qui-quadrado com 12 graus de liberdade é dado por

Considere que a variável aleatória X tem distribuição de Bernoulli com parâmetro p = 0,4. Sabe-se que a variável Y tem distribuição binomial com média igual a 2 e variância igual a 1. Supondo que X e Y são independentes, a probabilidade conjunta de X ser igual a zero e Y ser igual a 3, denotada por P(X = 0, Y = 3) é dada por
mostrar texto associado
Para fazer uma compra, via internet, uma pessoa escolhe entre duas grandes lojas de departamentos: A e B. Suponha que em 40% dos casos essa pessoa escolha a loja A e em 60% dos casos escolha a B. Suponha que o tempo de conexão, em minutos, para a efetivação da compra seja uma variável com distribuição exponencial com médias 5 minutos e 4 minutos, respectivamente, para a compra em A e B. Nessas condições, a probabilidade de ao fazer uma compra a loja escolhida ser B, dado que o tempo de efetivação da compra foi superior a 6 minutos é igual a
mostrar texto associado
Considere que a variável aleatória X tem distribuição de Poisson com média µ. Sabe-se que a variável aleatória Y tem distribuição uniforme contínua no intervalo [ -a, 2a ], onde a é um número real positivo, tem também média µ e variância igual a 3. Nessas condições, a probabilidade de X ser pelo menos 2 é igual a
© 2016-2025 Fonte Concursos - Questões de Concurso e Plano de Estudo