Questões de Concurso

Para prevenir que um ouvinte indesejado recupere informações, o transmissor codifica sua mensagem em palavras código utilizando uma chave secreta, que é conhecida pelo legítimo destinatário, mas não pelo ouvinte indesejado. Mensagens, palavras-código e chaves são representadas pelas variáveis aleatórias M, X e K, respectivamente, e se assume que K é independente de M. A função de codificação é representada por e: M x K → X, e a de decodificação é denotada por d: X x K → M. Nós nos referimos ao par (e, d) como um esquema de codificação.

BLOCH, M.; BARROS, J. Physical-layer security: from information theory to security engineering. Cambridge: Cambridge University Press,2011. Tradução livre.

Considere I(X; Y) = H(X) - H(X | Y), sendo X e Y duas variáveis discretas aleatórias. Acerca do vazamento de informação em uma comunicação, é correto afirmar que ele pode ser medido por

H(X) [entropia de Shannon] pode ser vista como uma medida da quantidade média de informação contida em X ou, de forma equivalente, a quantidade de incerteza que existe até o valor de X ser revelado.

BLOCH, M.; BARROS, J. Physical-layer security: from information theory to security engineering. Cambridge: Cambridge University Press,2011. Tradução livre.

Acerca da entropia de Shannon, e sendo X uma variável discreta aleatória, assinale a alternativa correta.

O número de empregados de uma empresa é igual a 200, sendo que 60% são homens e o restante mulheres. Nesta empresa, a média aritmética dos salários da população formada pelos salários dos homens é igual a 5 mil reais, com um coeficiente de variação igual a 30%, e a média aritmética dos salários da população formada pelos salários das mulheres também é igual a 5 mil reais, porém com um coeficiente de variação igual a 20%. Considerando a população formada por todos os 200 empregados da empresa, obtém-se que a variância, em mil reais ao quadrado, dos respectivos salários é igual a

Em um relatório de auditoria acerca de uma determinada ocorrência em 8 regiões, obteve-se o gráfico abaixo.
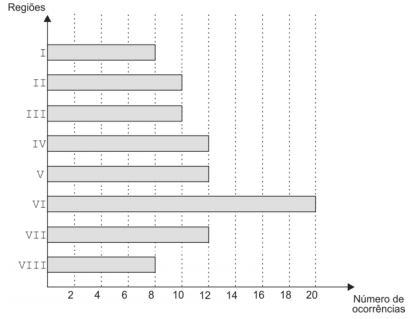Com relação a este relatório, sejam Md a mediana e Me a média aritmética (número de ocorrências por região) correspondentes. O valor da respectiva moda é, então, igual a

De uma amostra aleatória de tamanho 64 extraída, com reposição, de uma população normalmente distribuída e variância conhecida σ2, obteve-se um intervalo de confiança de 95% igual a [23,27] para a média μ desta população. Desejando-se obter um intervalo de confiança de 95% para μ, porém com amplitude igual à metade da obtida anteriormente, é necessário extrair da população uma amostra aleatória, com reposição, de tamanho