Questões de Concurso
Filtrar
708 Questões de concurso encontradas
Página 57 de 142
Questões por página:
Questões por página:
Concurso:
Prefeitura de Jandaia do Sul - PR
Disciplina:
Matemática
Uma caixa de 18 metros quadrados equivale a quantos centímetros quadrados?
Uma região plana foi delimitada por circunferência cujo comprimento era de, aproximadamente,157 m. A alternativa que mais se aproxima da área dessa região demarcada é:
Concurso:
Prefeitura Municipal de Horizontina - RS
Disciplina:
Matemática
Considerando que o círculo I possui raio igual a 4 cm e o círculo II tem raio igual a 5 cm, o valor da área do círculo II subtraída a área do círculo I é igual a: Utilize π = 3,14
Concurso:
Prefeitura de Dezesseis de Novembro - RS
Disciplina:
Matemática
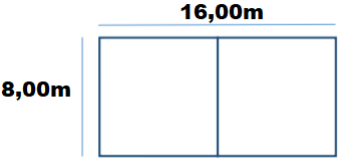
Calcule a área da quadra de tênis representada pela imagem abaixo:

Concurso:
Câmara de São Miguel da Boa Vista - SC
Disciplina:
Matemática
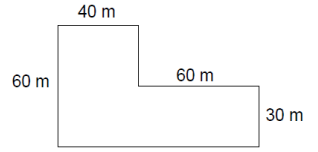
A figura abaixo representa um terreno que deve ser asfaltado para a construção de um galpão industrial. Tendo em vista as medidas representadas pelo desenho, assinalar a alternativa que apresenta a área total que deve ser asfaltada: