Questões de Concurso

A figura a seguir refere-se a três sólidos com raio = 1/6 de 36 cm; a altura do cilindro é 1/2 do raio mais 1 cm e a altura do cone é o dobro da altura do cilindro.

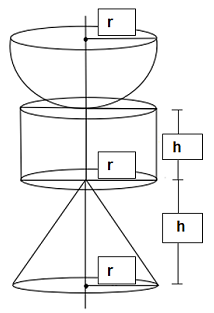
Julgue o seguinte item, relativo a geometria espacial.

Suponha que uma casquinha de sorvete tenha forma de cone circular reto com raio r e altura r. Suponha também que se deseje preencher essa casquinha com chocolate de tal forma que, após o preenchimento, caiba exatamente no espaço restante dentro da casquinha metade de uma bola de sorvete, em forma de uma semiesfera de raio 2r/3, posicionada de cabeça para baixo. Nesse caso, é correto afirmar que o volume de chocolate necessário para preencher o espaço dentro dessa casquinha de modo a satisfazer essa condição é igual a 11 πr³/81.

Como é e para que serve prioritariamente uma xícara todos sabemos: Servir bebidas, especialmente quentes. Mas de onde surgiu a ideia de criar um "copo com alça"?

O chá, que tem origem oriental, era inicialmente servido em potes redondos, sem alças. Segundo a tradição, isso era até mesmo um alerta para quem conduzia a cerimônia da bebida: Caso o recipiente queimasse as pontas dos dedos, estava quente demais para ser ingerido. Na temperatura ideal, ela não incomodava, mesmo com o contato direto com a porcelana.

Fonte: http://www.mexidodeideias.com.br/viagem/a-historia-da-xicara. Acesso em 06/01/2018.

Uma xícara de chá tem a forma de um tronco de cone reto, conforme a figura abaixo. Qual o volume máximo, aproximado, de líquido que ela pode conter?