Filtrar
325 Questões de concurso encontradas
Página 1 de 65
Questões por página:
Questões por página:
Concurso:
Prefeitura de Capanema - PR
Disciplina:
Física
Os satélites artificiais não caem sobre a Terra porque
Concurso:
Prefeitura de Capanema - PR
Disciplina:
Física
De acordo com a 1.ª lei de Newton, um corpo
Concurso:
Prefeitura de Capanema - PR
Disciplina:
Física
Em determinada avenida, o motorista de um veículo coletivo fez uma manobra em curva, e um passageiro teve a sensação de que uma força o estava empurrando para fora da curva.
Considerando a situação hipotética precedente, julgue os itens a seguir.
I A sensação descrita pelo passageiro é causada por uma força centrífuga real que atua sobre ele.
II A força que mantém o veículo na trajetória curva é a força centrípeta, cujo vetor aponta para o ponto central da curva.
III A sensação descrita pelo passageiro é explicada pelo princípio da inércia, pois o corpo tende a manter sua trajetória retilínea.
IV Como o veículo é um referencial não inercial, a sensação descrita pelo passageiro só poderá ser explicada caso seja introduzida uma força fictícia.
Estão certos apenas os itens
Considerando a situação hipotética precedente, julgue os itens a seguir.
I A sensação descrita pelo passageiro é causada por uma força centrífuga real que atua sobre ele.
II A força que mantém o veículo na trajetória curva é a força centrípeta, cujo vetor aponta para o ponto central da curva.
III A sensação descrita pelo passageiro é explicada pelo princípio da inércia, pois o corpo tende a manter sua trajetória retilínea.
IV Como o veículo é um referencial não inercial, a sensação descrita pelo passageiro só poderá ser explicada caso seja introduzida uma força fictícia.
Estão certos apenas os itens
Concurso:
Prefeitura de Catalão - GO
Disciplina:
Física
Durante o processo de tratamento de água em uma estação de abastecimento, é comum o uso de bombas hidráulicas para transportar o líquido entre diferentes reservatórios. A eficiência energética desses sistemas é essencial para reduzir o consumo de energia elétrica e os impactos ambientais. Uma bomba hidráulica eleva água de um reservatório inferior para um reservatório superior, situado a 10 metros de altura. Sabendo que a densidade da água é de aproximadamente 1000kg/m3 e que a aceleração da gravidade é 9,8m/s2, qual é o trabalho necessário para elevar 500 litros de água até o reservatório superior, desconsiderando perdas por atrito?
Analise o diagrama vetorial que representa forças atuando sobre um corpo de 500 gramas de massa. Observe. 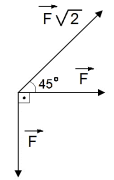
Desconsiderando o atrito, o valor em módulo da aceleração em m/s2 deste corpo na direção e no sentido da força resultante do sistema é:

Desconsiderando o atrito, o valor em módulo da aceleração em m/s2 deste corpo na direção e no sentido da força resultante do sistema é: