Questões de Concurso
Filtrar
568 Questões de concurso encontradas
Página 67 de 114
Questões por página:
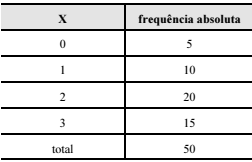
Considerando que a tabela precedente mostra a distribuição de frequências de uma variável quantitativa X, julgue o item a seguir.
A média amostral da variável em tela é inferior a 2.
Considerando que a tabela precedente mostra a distribuição de frequências de uma variável quantitativa X, julgue o item a seguir.
A moda e a mediana da variável X são, respectivamente, iguais a 2 e 1,5.
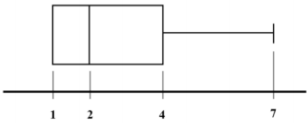
Considerando que uma variável quantitativa discreta X se distribui conforme o diagrama boxplot anterior, julgue o item seguinte.
As observações da variável X que assumem valores iguais a 7, com base nesse diagrama boxplot, são considerados outliers.
Considerando que uma variável quantitativa discreta X se distribui conforme o diagrama boxplot anterior, julgue o item seguinte.
O diagrama boxplot indica que o intervalo interquartil (ou interquartílico) da distribuição da variável X é igual a 3.
Considerando que uma variável quantitativa discreta X se distribui conforme o diagrama boxplot anterior, julgue o item seguinte.
1/3 das observações da variável X são iguais a 7.