Questões de Concurso
Filtrar
566 Questões de concurso encontradas
Página 9 de 114
Questões por página:
Questões por página:
No curso de Design Gráfico de um colégio técnico estão matriculadas no período noturno 60 pessoas sendo 28 mulheres e 32 homens, e as frequências desses alunos em uma determinada semana do mês de outubro estão representadas no gráfico de colunas a seguir. 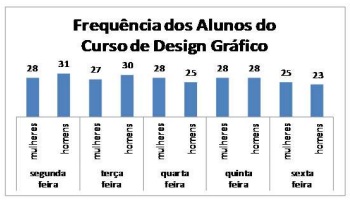
Como podemos observar, no topo de cada coluna desse gráfico está informado o número de alunos presentes naquele referido dia da semana, identificando a quantidade de mulheres e homens presentes naquele dia.
Analisando a distribuição dos alunos presentes no curso conforme apresentado no gráfico, podemos concluir como verdadeira qual das afirmações a seguir:

Como podemos observar, no topo de cada coluna desse gráfico está informado o número de alunos presentes naquele referido dia da semana, identificando a quantidade de mulheres e homens presentes naquele dia.
Analisando a distribuição dos alunos presentes no curso conforme apresentado no gráfico, podemos concluir como verdadeira qual das afirmações a seguir:
Concurso:
Prefeitura de Guarulhos - SP
Disciplina:
Estatística
No curso de Design Gráfico de um colégio técnico estão matriculadas no período noturno 60 pessoas sendo 28 mulheres e 32 homens, e as frequências desses alunos em uma determinada semana do mês de outubro estão representadas no gráfico de colunas a seguir.
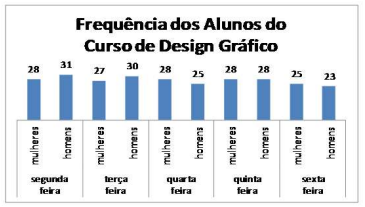
Como podemos observar, no topo de cada coluna desse gráfico está informado o número de alunos presentes naquele referido dia da semana, identificando a quantidade de mulheres e homens presentes naquele dia.
Analisando a distribuição dos alunos presentes no curso conforme apresentado no gráfico, podemos concluir como verdadeira qual das afirmações a seguir:

Como podemos observar, no topo de cada coluna desse gráfico está informado o número de alunos presentes naquele referido dia da semana, identificando a quantidade de mulheres e homens presentes naquele dia.
Analisando a distribuição dos alunos presentes no curso conforme apresentado no gráfico, podemos concluir como verdadeira qual das afirmações a seguir:
Concurso:
Prefeitura de Guarulhos - SP
Disciplina:
Estatística
No curso de Design Gráfico de um colégio técnico estão matriculadas no período noturno 60 pessoas sendo 28 mulheres e 32 homens, e as frequências desses alunos em uma determinada semana do mês de outubro estão representadas no gráfico de colunas a seguir.
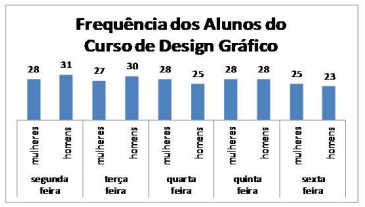
Como podemos observar, no topo de cada coluna desse gráfico está informado o número de alunos presentes naquele referido dia da semana, identificando a quantidade de mulheres e homens presentes naquele dia.
Analisando a distribuição dos alunos presentes no curso conforme apresentado no gráfico, podemos concluir como verdadeira qual das afirmações a seguir:

Como podemos observar, no topo de cada coluna desse gráfico está informado o número de alunos presentes naquele referido dia da semana, identificando a quantidade de mulheres e homens presentes naquele dia.
Analisando a distribuição dos alunos presentes no curso conforme apresentado no gráfico, podemos concluir como verdadeira qual das afirmações a seguir:
Concurso:
Prefeitura de Guarulhos - SP
Disciplina:
Estatística
No curso de Design Gráfico de um colégio técnico estão matriculadas no período noturno 60 pessoas sendo 28 mulheres e 32 homens, e as frequências desses alunos em uma determinada semana do mês de outubro estão representadas no gráfico de colunas a seguir.
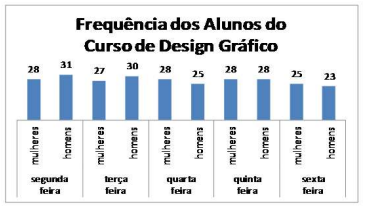
Como podemos observar, no topo de cada coluna desse gráfico está informado o número de alunos presentes naquele referido dia da semana, identificando a quantidade de mulheres e homens presentes naquele dia.
Analisando a distribuição dos alunos presentes no curso conforme apresentado no gráfico, podemos concluir como verdadeira qual das afirmações a seguir:

Como podemos observar, no topo de cada coluna desse gráfico está informado o número de alunos presentes naquele referido dia da semana, identificando a quantidade de mulheres e homens presentes naquele dia.
Analisando a distribuição dos alunos presentes no curso conforme apresentado no gráfico, podemos concluir como verdadeira qual das afirmações a seguir:
De acordo com o Censo 2022, realizado pelo IBGE, observe a Pirâmide Etária abaixo:
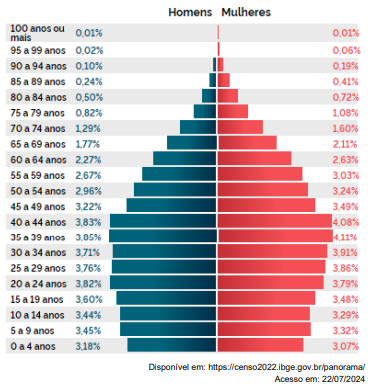
Diante do exposto, é INCORRETO afirmar que: