Questões de Concurso
Filtrar
215 Questões de concurso encontradas
Página 28 de 43
Questões por página:
Questões por página:
Seja f(X) = 2X² + X + 4; então, sobre sua representação gráfica, podemos afirmar que:
O gráfico da função f(X) = 10.X² - 12.X, corta o eixo dos X nos pontos:
Concurso:
AL-SP
Disciplina:
Matemática
O gráfico a seguir representa a função f, de domínio real, dada pela lei 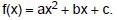
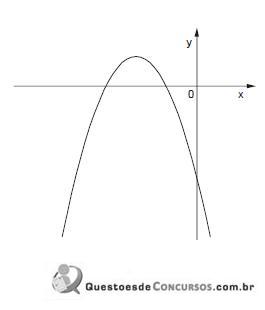
Sabendo que a, b e c são constantes, é correto concluir que
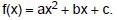

Sabendo que a, b e c são constantes, é correto concluir que
Concurso:
AL-SP
Disciplina:
Matemática
O gráfico a seguir representa a função f, de domínio real, dada pela lei f(x) = ax2 + bx + c.
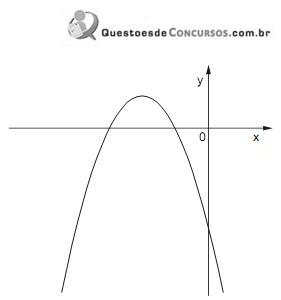
Sabendo que a, b e c são constantes, é correto concluir que

Sabendo que a, b e c são constantes, é correto concluir que
Concurso:
AL-RO
Disciplina:
Matemática
A distância focal da elipse x2 + 5y2 = 100 é