2. Questões de Concurso

Filtrar

Questões por página:
Sabe-se que x e y são números reais tais que y = 53x .
Conclui-se que x é igual a

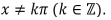
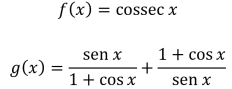
Considere as funções reais f e g, definidas a seguir para todo Imagem associada para resolução da questão



Imagem associada para resolução da questão




Considere agora a função h definida por h(x) = f(x) + g(x). O menor valor positivo pertencente ao conjunto imagem de h é igual a:

Considere que T semanas após a data em que foram diagnosticados os primeiros 300 casos de uma epidemia, o número N de pessoas infectadas seja dado pela função N(T)=300×20,8T.

Dessa forma, o número de semanas passadas, após o diagnóstico dos primeiros 300 casos, para que o total de infectados fosse igual a 4.800, é igual a:
Em uma reserva florestal, um grupo de ambientalistas está monitorando uma espécie de planta cuja população diminui devido a condições ambientais adversas. Os ambientalistas preveem que a quantidade dessas plantas diminuirá ao longo do tempo de acordo com a seguinte lei de decaimento:
P(t)= P(0)*4^(- t/3) em que P(0) é a quantidade estimada de plantas antes do início das condições adversas e P(t) é a quantidade restante após t anos. Qual é o tempo necessário, desde o início dessas condições, para que a população de plantas se reduza a 1/8 da população inicial?
Em um laboratório de pesquisa sobre insetos, constatou-se que a população P de um determinado tipo de formiga cresce de acordo com a expressão P(t) = 25*2^t, em que “t” representa o tempo em horas. Para atingir uma população de 200 formigas, será necessário um tempo de:
© 2016-2025 Fonte Concursos - Questões de Concurso e Plano de Estudo