Questões de Concurso
Filtrar
115 Questões de concurso encontradas
Página 18 de 23
Questões por página:
Teste de Hipótese compõe um conjunto de regras de decisão para aceitar ou rejeitar uma hipótese estatística com base em dados amostrais. A respeito do Teste de Hipótese, avalie as considerações a seguir.
I. A hipótese utilizada como referência no teste é a hipótese nula, representada pela sigla H0.
II. A construção da região crítica é feita sob a premissa de que a hipótese utilizada como referência é falsa.
III. Ao se testar a hipótese utilizada como referência, está sujeito a cometer dois tipos de erros: rejeitar a hipótese quando ela é verdadeira, ou não rejeitar a hipótese quando ela é falsa.
IV. Em caso de teste para diferença entre médias de duas populações normais, a hipótese alternativa assumira a igualdade entre as duas médias.
V. Na construção da região crítica com teste bilateral, o nível de significância deve ser dividido entre as duas áreas de rejeição.
É CORRETO apenas o que se afirma em:
Considere as seguintes afirmações.
I. Quando a hipótese nula é falsa, a estimativa dos tratamentos-entre superestima a variância resultando em valores maiores para Fteste .
II. Na análise da variância a estatística Fteste é obtida pelo quociente 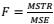
III. Na análise da variância a estatística Fteste é obtida pelo quociente 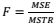
IV. Quando a hipótese nula é falsa, a estimativa dos tratamentos-entre tem variância menor resultando em valores menores para a estatística Fteste .
V. A regra de rejeição de Ho é definida por Fteste < Fcritico
Assinale a alternativa que indica apenas as assertivas CORRETAS.
Durante o processo produtivo uma amostra é colhida para inspeção de determinada peça fornecidas para montadoras de racks metálicos. As medidas de uma amostra foram realizadas no processo de inspeção, resultando nos seguintes dados (em mm): (Wcrítico,0,05 =13).
0,448; 0,451; 0,453; 0,449; 0,447; 0,448; 0,453;0,452; 0,453; 0,450; 0,449 e 0,447
Utilizando-se do teste de Wilcoxon do posto sinalizado, avaliar a amostra para verificar se o diâmetro médio das peças é de 0,449 mm.
Um modelo de regressão linear múltipla tem a forma y = β0 + β1X1 + β2X2 + ε, em que β0, β1 e β2 são os coeficientes do modelo e ε denota o erro aleatório normal com média nula e desvio padrão σ. As variáveis regressoras X1 e X2 são ortogonais. O quadro a seguir mostra as estimativas dos coeficientes do modelo obtidas pelo método da máxima verossimilhança a partir de uma amostra de tamanho n = 20. Nesse quadro, para cada coeficiente βk, k = 0,1,2, a razão t refere-se ao seu teste de significância H0 : βk = 0 versus H1 : βk ≠ 0.
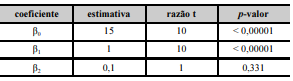
Com base nessas informações e no quadro apresentado, julgue o próximo item.
A hipótese nula H0 : β2 = 0 é rejeitada para o nível de significância do teste α = 5%.