Questões de Concurso
Filtrar
65 Questões de concurso encontradas
Página 10 de 13
Questões por página:
Questões por página:
Concurso:
PM-MG
Disciplina:
Matemática
Resolvendo a equação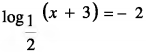 , temos:
, temos:
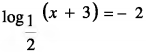 , temos:
, temos:
Concurso:
PM-ES
Disciplina:
Matemática
mostrar texto associado
Tomando 0,301 e 0,477 como os valores aproximados de log10 2 e log10 3, respectivamente, é correto inferir que log10 72 = 1,578.
Concurso:
PM-ES
Disciplina:
Matemática
mostrar texto associado
Se log5 b = 0,1, em que b é um número positivo, então logb 25=0,01.
Sendo log 2 = 0,30 e log 3 = 0,47, o conjunto solução da expressão E = log 2.108 + log 3.10- 5 é:
Sobre propriedades de logaritmos, marque V para as verdadeiras e F para as falsas.
( ) Sendo a, b e c números reais positivos, a ≠ 1, então: loga (b.c) = logab − logac.
( ) Sendo a e b números reais positivos, a ≠ 1, e m um número real então: loga bm = m loga b.
( ) Sendo a, b e c números reais positivos, a ≠ 1, então: loga (b/c)= loga b + loga c.
Assinale a sequência correta.