Questões de Concurso
Filtrar
139 Questões de concurso encontradas
Página 23 de 28
Questões por página:
Na seguinte matriz, em cada linha, estão anotadas as notas obtidas por quatro soldados em três provas durante o decorrer da semana em atividades internas no quartel. Por exemplo, o soldado 1 obteve nota 70 na prova 1, nota 80 na prova 2 e nota 90 na prova 3.

Sabendo que se obtém a nota final de cada soldado somando-se suas três notas obtidas e, em seguida, dividindo-se o resultado obtido dessa soma por 4, é correto afirmar que
Para saber o custo total (em reais) na produção de x uniformes para um grupo de soldados, primeiramente substitui-se cada elemento x, da matriz a seguir, pela quantidade de uniformes que se quer produzir e calcula-se o determinante dessa matriz, obtendo-se, assim, o custo total na produção destes x uniformes igual ao valor do determinante.
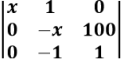
Dessa forma, para se produzir 70 uniformes para um grupo de soldados, o custo total nessa produção será de
Considere as duas matrizes A e B a seguir:

Cada linha da matriz A indica a pontuação obtida, em cada tentativa, em uma prova de tiro ao alvo por um competidor. Assim, a primeira linha indica as pontuações do competidor X, a segunda linha indica as pontuações do competidor Y e a terceira linha indica as pontuações do competidor Z. Obtendo-se uma matriz C = A.B, na matriz C aparece a nota de desempenho final de cada um dos três competidores X, Y e Z, respectivamente, na primeira, na segunda e na terceira linha.
Dessa forma, é correto afirmar que
Considere as duas matrizes 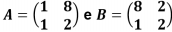 . Sendo C uma nova matriz tal que C = 3B – 2A, então a soma dos elementos da matriz C é igual a
. Sendo C uma nova matriz tal que C = 3B – 2A, então a soma dos elementos da matriz C é igual a
A matriz transposta de 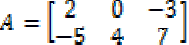 é a matriz:
é a matriz: