Questões de Concurso
Filtrar
39 Questões de concurso encontradas
Página 4 de 8
Questões por página:
Questões por página:
Concurso:
Prefeitura de Cuiabá - MT
Disciplina:
Estatística
Questão Anulada
Suponha que foi aplicado um modelo de regressão linear simples em um conjunto de n pares de valores da forma (x_i, y_i), i=1, ..., n. Sejam ?x e ?y as médias dos valores x_i e y_i, i=1, ..., n, respectivamente. Sabe-se que:
(i) ?x=0,25 (ii) ?y=0,75 (iii) ∑_(i=1)^n??(x_i-?x)(y_i-?y)?=12 (iv) ∑_(i=1)^n??(x_i-?x )^2 ?=2
Considerando os dados acima, a equação resultante da regressão linear é dada por
(i) ?x=0,25 (ii) ?y=0,75 (iii) ∑_(i=1)^n??(x_i-?x)(y_i-?y)?=12 (iv) ∑_(i=1)^n??(x_i-?x )^2 ?=2
Considerando os dados acima, a equação resultante da regressão linear é dada por
Concurso:
Prefeitura de Cuiabá - MT
Disciplina:
Estatística
Considere dois conjuntos de dados distintos, denotados por C1 e C2, ambos do mesmo tamanho, isto é, com a mesma quantidade de valores. A cada conjunto foi aplicado o mesmo método de regressão linear. O erro médio quadrático obtido para C1 foi menor do que para C2. Com base no exposto, analise as afirmativas a seguir, e assinale V para a afirmativa verdadeira e F para a falsa.
( ) O erro médio quadrático é uma métrica típica de erro em problemas de regressão cujo valor varia entre 0 e 1.
( ) Pode-se afirmar que o conjunto de dados C1 está melhor ajustado ao modelo do que o conjunto de dados C2.
( ) Pode-se afirmar que para melhorar o ajuste do conjunto de dados C2 é preciso aumentar seu tamanho.
As afirmativas são, respectivamente,
( ) O erro médio quadrático é uma métrica típica de erro em problemas de regressão cujo valor varia entre 0 e 1.
( ) Pode-se afirmar que o conjunto de dados C1 está melhor ajustado ao modelo do que o conjunto de dados C2.
( ) Pode-se afirmar que para melhorar o ajuste do conjunto de dados C2 é preciso aumentar seu tamanho.
As afirmativas são, respectivamente,
Três funcionários de uma sociedade empresária executam uma mesma tarefa rotineira, mas importante para o faturamento da sociedade.
O tempo médio de execução da tarefa dos funcionários, em minutos, e suas respectivas variâncias, estão na tabela abaixo.
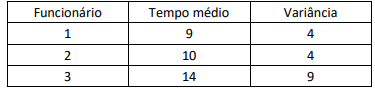
Sobre a variabilidade relativa da execução da tarefa, assinale a afirmativa correta.
O tempo médio de execução da tarefa dos funcionários, em minutos, e suas respectivas variâncias, estão na tabela abaixo.

Sobre a variabilidade relativa da execução da tarefa, assinale a afirmativa correta.
Concurso:
EBSERH
Disciplina:
Estatística
As variáveis número de horas de treinamento preventivo e número de acidentes de trabalho foram analisadas e forneceram a seguinte equação de regressão linear: Y previsto = 8,5 – 0,006X. Esta equação permite afirmar que:
Em um modelo de regressão linear múltipla, os valores da variável aleatória Y são previstos com base em valores observados da variável X = [X1, X2, X3], em que βi, i = 1,2, …, n, corresponde ao i-ésimo parâmetro do modelo e ε ao erro aleatório. O modelo linear com todas as variáveis independentes é: