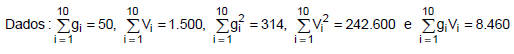Questões de Concurso
Filtrar
118 Questões de concurso encontradas
Página 15 de 24
Questões por página:
Questões por página:
Concurso:
TCM-SP
Disciplina:
Estatística
Uma cuidadosa pesquisa de preços sobre os custos da construção civil, mais especificamente para a edificação de certos tipos de infraestruturas públicas, demonstrou que o valor por metro quadrado tem distribuição próxima da Normal com média de R$1.600 e variância 14.400. São fornecidos também valores da distribuição normal padrão e respectivas probabilidades, conforme abaixo:
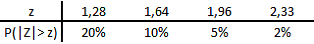
Suponha que, para fins de fiscalização, o Tribunal de Contas do Município de São Paulo tenha convencionado que, dentre todas as obras, as 10% mais caras deveriam passar por um exame ainda mais detalhado. Então, isso significa que o critério estabelecido determina, estatisticamente, que uma obra deverá receber um tratamento mais rigoroso quando o custo por metro quadrado for superior a:
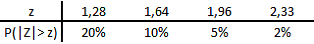
Suponha que, para fins de fiscalização, o Tribunal de Contas do Município de São Paulo tenha convencionado que, dentre todas as obras, as 10% mais caras deveriam passar por um exame ainda mais detalhado. Então, isso significa que o critério estabelecido determina, estatisticamente, que uma obra deverá receber um tratamento mais rigoroso quando o custo por metro quadrado for superior a:
Concurso:
TRT - 14ª Região (RO e AC)
Disciplina:
Estatística
Dois grupos independentes (G1 e G2) são formados por trabalhadores de uma cidade. G1 é composto por uma amostra aleatória, com reposição, de 100 empregados da empresa E1 e G2 por uma amostra aleatória, com reposição, de 60 empregados de uma outra empresa E2. Deseja-se testar a hipótese, utilizando a distribuição qui-quadrado, se as medianas dos salários dos empregados de G1 e G2 são iguais ao nível de significância de 5%. Foram formuladas então as hipóteses H0: As medianas de G1 e G2 são iguais (hipótese nula) e H1: As medianas de G1 e G2 são diferentes (hipótese alternativa).
A tabela abaixo apresenta o resultado de um levantamento realizado com relação à mediana (Md) dos salários do grupo combinado (das duas amostras juntas).

Dados: Valores críticos (c) da tabela da distribuição qui-quadrado com n graus de liberdade para α = 0,05, tal que a probabilidade P(qui-quadrado > c) = 0,05.

A conclusão do teste é que H0
A tabela abaixo apresenta o resultado de um levantamento realizado com relação à mediana (Md) dos salários do grupo combinado (das duas amostras juntas).

Dados: Valores críticos (c) da tabela da distribuição qui-quadrado com n graus de liberdade para α = 0,05, tal que a probabilidade P(qui-quadrado > c) = 0,05.

A conclusão do teste é que H0
Concurso:
TRT - 11ª Região (AM e RR)
Disciplina:
Estatística
mostrar texto associado
Para testar a existência da regressão, ao nível de significância α, optou-se pelo teste t de Student, com a formulação das hipóteses: H₀: β = 0 (hipótese nula) contra H1: β ≠ 0 (hipótese alternativa). A estatística tc (t calculado), utilizada para a conclusão do teste, apresentou então um valor igual a
Concurso:
TRT - 11ª Região (AM e RR)
Disciplina:
Estatística
A variância de uma população de tamanho infinito, normalmente distribuída com média μ, é desconhecida. Deseja-se testar as hipóteses H₀: μ = 12 (hipótese nula) contra H₁: μ > 12 (hipótese alternativa), ao nível de significância α, com a utilização do teste t de Student. Para isto, foi extraída da população uma amostra aleatória de tamanho 9 obtendo-se uma média amostral igual a 12,8 e uma variância amostral igual a 1,44. Considere que tα é o quantil da distribuição t de Student para o teste unicaudal tal que a probabilidade P(t > tα) = α, com n graus de liberdade.
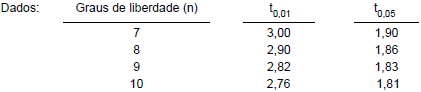
É correto afirmar que H₀

É correto afirmar que H₀
Concurso:
TRT - 11ª Região (AM e RR)
Disciplina:
Estatística
Uma população P de tamanho infinito tem distribuição normal com média μ e variância 2,25. A fim de proceder ao teste H₀: μ = 10 (hipótese nula) contra H₁: μ ≠ 10 (hipótese alternativa), ao nível de significância de 5%, extrai-se de P uma amostra aleatória de tamanho 100, estabelecendo-se a seguinte regra: “dado que 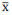 é a média da amostra, então rejeita-se H₀ se
é a média da amostra, então rejeita-se H₀ se 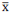 < 10 − K ou
< 10 − K ou 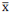 > 10 + K, em que K > 0”. Considerando que na curva normal padrão (Z) as probabilidades P(|Z| > 1,96) = 0,05 e P(|Z| > 1,64) = 0,10, obtém-se que o valor de K é
> 10 + K, em que K > 0”. Considerando que na curva normal padrão (Z) as probabilidades P(|Z| > 1,96) = 0,05 e P(|Z| > 1,64) = 0,10, obtém-se que o valor de K é
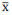 é a média da amostra, então rejeita-se H₀ se
é a média da amostra, então rejeita-se H₀ se 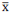 < 10 − K ou
< 10 − K ou 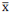 > 10 + K, em que K > 0”. Considerando que na curva normal padrão (Z) as probabilidades P(|Z| > 1,96) = 0,05 e P(|Z| > 1,64) = 0,10, obtém-se que o valor de K é
> 10 + K, em que K > 0”. Considerando que na curva normal padrão (Z) as probabilidades P(|Z| > 1,96) = 0,05 e P(|Z| > 1,64) = 0,10, obtém-se que o valor de K é