Questões de Concurso
Filtrar
522 Questões de concurso encontradas
Página 33 de 105
Questões por página:
Questões por página:
Concurso:
Prefeitura de Vila Boa - GO
Disciplina:
Matemática
Em uma brincadeira infantil, as crianças precisavam coletar pedras coloridas que estavam escondidas em um parque, e cada pedra tinha uma pontuação única baseada em sua cor. O quadro abaixo mostra a relação das pedras e os seus respectivos pontos.
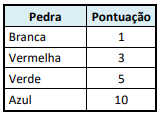
Valentina, uma das crianças que participou da brincadeira, conseguiu coletar 7 pedras brancas,3 pedras vermelhas,3 pedras verdes e 2 pedras azuis. Assinalar a alternativa que corresponde à quantidade de pontos que Valentina fez.

Valentina, uma das crianças que participou da brincadeira, conseguiu coletar 7 pedras brancas,3 pedras vermelhas,3 pedras verdes e 2 pedras azuis. Assinalar a alternativa que corresponde à quantidade de pontos que Valentina fez.
Concurso:
Prefeitura de Macaé - RJ
Disciplina:
Matemática
Este mês, Delvina gastou dois quintos do seu salário fazendo as compras do mês no supermercado. Do que sobrou, ela gastou dois terços pagando o aluguel. Daquilo que sobrou depois desses dois gastos, um quarto foi destinado à conta de energia elétrica, no valor de R$230,00.
É correto afirmar que Delvina
É correto afirmar que Delvina
Concurso:
Prefeitura de Nina Rodrigues - MA
Disciplina:
Matemática
Certo dia, Lucas e Daniele competiram em um jogo de celular. Lucas conseguiu marcar 240 pontos jogando por um minuto. Quanto tempo levou para que Daniele marcasse 220 pontos sabendo que o rendimento de ambos era igual?
Concurso:
Prefeitura de Cacimba de Dentro - PB
Disciplina:
Matemática
Letícia é filha de Carlos e está aguardando para receber a vacina da COVID-19. A prefeitura da cidade onde eles moram estabeleceu o seguinte calendário de vacinação:

Sabendo que a razão das idades de Letícia e Carlos é de dois para sete e que a soma de suas idades é 81, qual o período em que Letícia poderá ser vacinada?

Sabendo que a razão das idades de Letícia e Carlos é de dois para sete e que a soma de suas idades é 81, qual o período em que Letícia poderá ser vacinada?
Concurso:
Prefeitura de Cruz Alta - RS
Disciplina:
Matemática
São exemplos de operações lógicas com resultados verdadeiros:
I. Se 8 + 8 = 16, então 3 x 4 = 9.
II.12 ÷ 3 = 4 ou 5 x 9 = 45.
III.4 x 6 = 24 e 3 x 8 = 24.
Quais estão corretas?