Questões de Concurso
Filtrar
91 Questões de concurso encontradas
Página 1 de 19
Questões por página:
Questões por página:
Boa parte dos torcedores acha que, se um jogador está machucado, não é possível ganhar o campeonato. Ao considerar falsa a afirmação “Se Neymar está machucado, então o Brasil não ganha o campeonato”, assinale a alternativa que é, necessariamente verdadeira:
Concurso:
Prefeitura de Gameleira de Goiás - GO
Disciplina:
Raciocínio Lógico
Considere as proposições compostas:
• (P ∧ Q) → (P ∨ Q). • (P ∨ Q) → (P ∧ Q).
Essas proposições são, respectivamente, exemplos de
• (P ∧ Q) → (P ∨ Q). • (P ∨ Q) → (P ∧ Q).
Essas proposições são, respectivamente, exemplos de
Concurso:
Câmara de Porto Velho - RO
Disciplina:
Raciocínio Lógico
Analise as fórmulas a seguir:
I) A ∨ ¬B
II) ((A → B) ∧ B) → A
III) ((A ∨ B) ∧ ¬A) ∧ ¬A
IV) ((A → B) ∧ (C → D)) ∧ ¬(A → D)
V) P → ¬(P ∨ P)
São tautologias:
I) A ∨ ¬B
II) ((A → B) ∧ B) → A
III) ((A ∨ B) ∧ ¬A) ∧ ¬A
IV) ((A → B) ∧ (C → D)) ∧ ¬(A → D)
V) P → ¬(P ∨ P)
São tautologias:
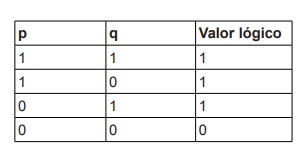
Analise a tabela a seguir, identifique qual operação lógica foi realizada e assinale a alternativa correta.
Disciplina:
Raciocínio Lógico
Considere as seguintes afirmativas:
A1 : A camiseta da seleção brasileira é branca ou a bermuda da seleção brasileira é amarela.
A2 : Se a bola da Copa é preta, então a bandeirinha do escanteio é listrada.
Sabe-se que ambas as afirmações são falsas. Então conclui-se que
