2. Questões de Concurso

Filtrar

Questões por página:
Um arquiteto está projetando uma estrutura e precisa determinar o valor de um ângulo interno de um triângulo. Se os dois primeiros ângulos medem 58° e 72°, qual é a medida do terceiro ângulo?
Visualizar Questão Comentada
Os lados de um triângulo medem, respectivamente, 4,7 e 9 cm. O perímetro do triângulo semelhante ao dado cujo lado maior é de 27cm, mede:
Visualizar Questão Comentada
Os pontos A, B, C, e D representam, nesta ordem, os vértices de um retângulo, e os pontos E e F são os pontos médios dos lados CD e AD, respectivamente. Sabendo que a área do triângulo BCE é igual a 220 cm2, então a área do triângulo ABF, em cm2, é igual a
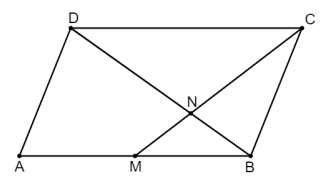
Um terreno tem o formato de um paralelogramo ABCD, como indicado na figura abaixo. O dono desse terreno pretende colocar cerâmica na parte indicada pelo quadrilátero AMND. Se M é o ponto médio de ̅AB, a área do triângulo MNB é 15 m2 e um metro quadrado da cerâmica usada custa R$ 30,00, então qual o valor, em reais, que o proprietário vai gastar com a cerâmica?

Imagem associada para resolução da questão
Alexandre queria saber qual a altura de um prédio, para isso mediu a sombra do prédio no momento em que o Sol estava a 60° acima do horizonte, conforme ilustra a figura abaixo. Sabendo que a sombra do prédio tinha 28,5 metros responda, qual a altura do prédio?
Imagem associada para resolução da questão
(Considere os seguintes valores: sen 30°= 0,5 cos 30° = 0,87 tan 30° = 0,57)

Visualizar Questão Comentada
© 2016-2026 Fonte Concursos - Questões de Concurso e Plano de Estudo