O modelo de análise fatorial representa a estrutura de covariância entre muitas variáveis aleatórias 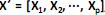, através de poucas variáveis não observáveis F´ = [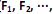 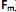] também conhecidas como fatores, construtos ou fatores comuns. Sendo E(X) = µ e V(X) = S, o modelo fatorial é expresso por X – µ = LF + e. A matriz 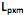é conhecida como matriz das cargas fatoriais e seus elementos, 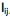, carga da variável i no fator j e as variáveis aleatórias F e em + p são não observáveis. Analise as afirmativas, marque V para as verdadeiras e F para as falsas.

( ) No modelo fatorial ortogonal, as variáveis não observáveis F e e são independentes, E(F) = 0, V(F) = E(F´F) = I, E(e) = 0, V(e) = E(e´e) = ψ. A matriz ψ é não diagonal, V(X) = S = L´L + ψ e Cov (X, F) = L.
( ) Um método de estimação para as cargas do modelo fatorial ortogonal é através de componentes principais, onde se utiliza a decomposição espectral da matriz S.
( ) Para se utilizar o método de máxima verossimilhança para estimar as cargas, é acrescida a suposição de que F e e têm distribuição normal multivariada. As comunalidades (elementos da diagonal LL´) têm como estimadores a proporção da variância total estimada pelo particular fator.
( ) Para melhorar a explicação do modelo fatorial, sem alterar a ortogonalidade dos fatores, muitas vezes, usa-se uma transformação ortogonal das cargas fatoriais, que, consequentemente, transforma os fatores. Esse procedimento é conhecido como rotação fatorial.
( ) Dependendo da natureza dos dados, os fatores não precisam ser ortogonais. Assim, para melhorar a explicação do modelo fatorial, pode-se utilizar a rotação oblíqua, onde cada variável é expressa em termos de um número máximo de fatores.
A sequência está correta em

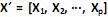O modelo de componentes principais é utilizado para representar a estrutura de variância-covariância em função de um número reduzido de combinações lineares das variáveis originais, com o objetivo de se ter uma redução de dados e uma melhor interpretação destes. Para o vetor aleatório com matriz de covariância S e autovalores iguais a 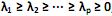, e as combinações lineares: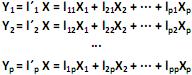



O modelo de componentes principais corresponde às combinações lineares não correlacionadas 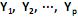com vetores de coeficientes 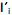de comprimento unitário, que apresentam as maiores variâncias Var 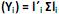. Diante do exposto, é correto afirmar que


I. o primeiro componente principal é a combinação linear 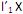que maximiza Var 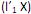sujeito a 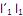= 1.

II. o i-ésimo componente principal é a combinação linear 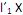que maximiza Var 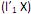= 1 e Cov (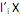, 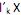) = 0, para k < i.

III. sendo 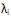os autovalores e ei os autovetores de S, o i-ésimo componente principal é dado por 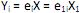+ , onde i = 1, ··· p.

IV. Var 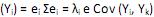= 0, para i = 1,2, ···, p e i ≠ k.

V. a proporção da variância total devido ao k-ésimo componente principal é dada por 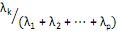para k = 1, ···, p.

Estão corretas apenas as afirmativas

“A análise de resíduos de um modelo de regressão linear múltipla pode ser utilizada para verificar se o modelo se adequa aos dados. Nesse sentido, gráficos e testes ajudam a identificar discrepâncias entre os valores observados da variável resposta e os valores preditos pelo modelo.” De acordo com o trecho anterior, marque V para as afirmativas verdadeiras e F para as falsas.

( ) Quando os pontos do diagrama de dispersão do resíduo padronizado versus variável explicativa apresentar uma tendência, a inclusão do logaritmo da variável explicativa pode melhorar o modelo.
( ) Quando os pontos do diagrama de dispersão do resíduo versus variável omitida no modelo apresentar uma tendência linear, a inclusão da variável omitida pode melhorar o modelo.
( ) Quando o desenho esquemático (boxplot) dos resíduos padronizados apresentar observações além dos limites superior ou inferior, existe uma forte indicação da presença de outliers que devem ser investigados.
( ) Quando o desenho esquemático dos resíduos tem a distância entre a mediana e o primeiro quartil e a distância entre a mediana e o terceiro quartil bem distintas, existe uma forte indicação de que a distribuição das observações são assimétricas e o componente aleatório do modelo pode não ter distribuição normal.
( ) A suposição de homocedasticidade dos resíduos pode ser avaliada através de: teste de Levéne; teste de Brown & Forsythe; gráfico de resíduos versus valores preditos pelo modelo; gráfico do resíduo versus cada uma das variáveis incluídas no modelo.

A sequência está correta em

Após o ajuste de um modelo de regressão linear múltipla, com n observações e k variáveis explicativas e o termo de intercepto, a tabela ANOVA pode ser utilizada na avaliação do modelo ajustado. As linhas da tabela ANOVA correspondem às fontes de variação devido à regressão, ao resíduo e ao total, e as colunas, aos graus de liberdade, as somas de quadrado, aos quadrados médios, a estatística F e ao valor p. Diante do exposto, analise.

I. O número de graus de liberdade da fonte regressão é k, da fonte resíduos é n-k-1 e do total é n-1.
II. O coeficiente de determinação múltipla corresponde à razão entre a soma de quadrados devido à regressão e à soma de quadrados total. Ele varia entre 0 e 1 e quanto mais próximo de 1, melhor é o modelo.
III. O coeficiente de determinação múltipla corrigido leva em consideração o número de observações e o número de variáveis explicativas incluídas no modelo e corresponde a 1 menos a razão entre o quadrado médio do resíduo e a soma de quadrado total dividida pelos seus graus de liberdade. Ele varia entre zero e 1 e quanto mais próximo de 1, melhor o modelo.
IV. A estatística F corresponde à razão entre o quadrado médio da regressão e o quadrado médio do resíduo e é utilizada para testar a significância do modelo ajustado quando comparado com o modelo nulo.
V. O valor p corresponde à probabilidade de significância ou ao nível descritivo do teste da estatística F, que é calculada utilizando a distribuição de Fisher-Snedecor com número de graus de liberdade iguais ao da fonte de variação da regressão e da fonte de variação do resíduo. Valores pequenos, em geral inferiores a 5%, são uma forte indicação de que o modelo é não significativo.

Estão corretas apenas as afirmativas

Em uma população finita de tamanho N, onde existem k indivíduos com uma característica de interesse, ao se selecionar uma amostra aleatória de tamanho n sem reposição, o número de indivíduos com a característica na amostra (R) é uma variável aleatória com distribuição hipergeométrica. A probabilidade de se ter exatamente r indivíduos na amostra com a característica de interesse é dada por

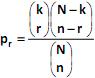, onde max (0, n – N + k) = r = min (k, n).

Analise.

I. Para N = 100, k = 20, n = 10 e r = 3, E(R) = 2 e Var(R) = 144/99.

II. Para N = 100, k = 20, n = 5 e r = 3, E(R) = 1 e Var(R) = 8/10.

III. Para N = 10000, k = 2000, n = 100 e r = 3, E(R) = 20 e Var(R) = 15,84.

IV. Para N = 10000, k = 1000, n = 100 e r = 3, E(R) = 10 e Var(R) ˜ 9.

V. Para N = 10000, k = 2000, n = 10 e r = 0, P(R = 0) ˜ 0,1074.

Estão corretas apenas as alternativas