Questões de Concurso
Filtrar
3.606 Questões de concurso encontradas
Página 149 de 722
Questões por página:
Questões por página:
Concurso:
TRT - 14ª Região (RO e AC)
Disciplina:
Estatística
Os estimadores independentes e não viesados E1, E2 e E3 são utilizados para a média μ de uma população normalmente distribuída e desvio padrão igual a 0,5. Tem-se que E1 = mX1 + nX2 − 2pX3, E2 = mX1 + 2nX2 − 4pX3 e E3 = 2mX1 + nX2 − 3pX3 sendo (X1, X2, X3) uma amostra aleatória simples com reposição da população e m, n e p parâmetros reais tal que n=2m=2p. Entre esses 3 estimadores, o mais eficiente apresenta uma variância igual a
Concurso:
TRT - 14ª Região (RO e AC)
Disciplina:
Estatística
A média de uma variável aleatória X, cuja distribuição é desconhecida, é igual a m, com m > 0. Pelo Teorema de Tchebichev, a probabilidade de X não pertencer ao intervalo (m − θ, m + θ), com m > θ, é no máximo igual a 16%. O desvio padrão de X é então igual a θ multiplicado por
Concurso:
TRT - 14ª Região (RO e AC)
Disciplina:
Estatística
Considere uma população P1 formada pela renda, em unidades monetárias (u.m.), dos 100 indivíduos que são sócios de um clube. Seja xi a renda, xi > 0, do sócio i.
Dados: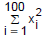
= 2.662.400 (u. m)2 e Coeficiente de variação de P1 igual a 20%.
Decide-se excluir de P1 um total de 20 sócios que possuem renda igual à média de P1, formando uma nova população P2 com tamanho 80. O módulo da diferença, em (u.m.)2, entre as variâncias de P1 e P2 é de
Dados:
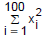= 2.662.400 (u. m)2 e Coeficiente de variação de P1 igual a 20%. Decide-se excluir de P1 um total de 20 sócios que possuem renda igual à média de P1, formando uma nova população P2 com tamanho 80. O módulo da diferença, em (u.m.)2, entre as variâncias de P1 e P2 é de
Concurso:
TRT - 14ª Região (RO e AC)
Disciplina:
Estatística
Analisando uma curva de frequência de uma distribuição estatística, observa-se que ela:
I. é unimodal. II. apresenta a moda menor que a mediana e a mediana menor que a média. III. possui os dados da distribuição fortemente concentrados em torno da moda.
Então, essa distribuição
I. é unimodal. II. apresenta a moda menor que a mediana e a mediana menor que a média. III. possui os dados da distribuição fortemente concentrados em torno da moda.
Então, essa distribuição
Concurso:
TRT - 14ª Região (RO e AC)
Disciplina:
Estatística
Seja a tabela de frequências relativas abaixo correspondendo à distribuição dos salários dos funcionários sem nível superior, lotados em um órgão público. Para o segundo e terceiro intervalos de classes não foram fornecidas as respectivas frequências (na tabela, denotadas por x e y, respectivamente).
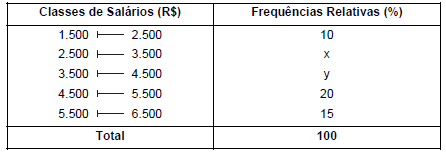
Utilizando o método da interpolação linear, obteve-se o valor de R$ 3.900,00 para a mediana (Md) dos salários. O valor da média aritmética (Me) foi obtido considerando que todos os valores incluídos em um certo intervalo de classe são coincidentes com o ponto médio deste intervalo. A expressão (3Md − 2Me) apresenta, em R$, um valor igual a
Utilizando o método da interpolação linear, obteve-se o valor de R$ 3.900,00 para a mediana (Md) dos salários. O valor da média aritmética (Me) foi obtido considerando que todos os valores incluídos em um certo intervalo de classe são coincidentes com o ponto médio deste intervalo. A expressão (3Md − 2Me) apresenta, em R$, um valor igual a
