2. Questões de Concurso

Filtrar

Questões por página:

O Teste de Kolmogorov-Smirnov de uma amostra é baseado na diferença entre duas funções: a Função Distribuição, F(x), e a Função Distribuição Empírica da amostra, definida como a proporção das observações da amostra menores ou iguais a 1. Com relação a esse teste, pode-se afirmar que a escala de medida da variável aleatória x deve ter seu nível de mensuração:

Com relação aos erros que podem ocorrer em um teste de hipóteses, pode-se afirmar que:

Em um modelo de regressão linear simples da forma Y = α + β X + μ, foram calculadas, pelo método de mínimos quadrados ordinários, as estimativas dos parâmetros obtendo-se Y = a + b X, cujo coeficiente de determinação é igual a 0,95. Isso significa que:

Três estimadores da média populacional - e1, e2, e3 - para amostras de tamanho n são calculados como segue: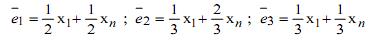



em que x1 e xnrepresentam, respectivamente, o menor e maior elemento da amostra. Entre esses estimadores, pode-se afirmar que:

A retirada de amostras aleatórias simples pode ser realizada segundo dois critérios, a saber: com ou sem reposição. Considerando-se uma população de tamanho N = 10 e amostras de tamanho n = 3, o número de possíveis amostras aleatórias simples que podem ser retiradas dessa população, utilizando-se os critérios com e sem reposição são, respectivamente, iguais a:
© 2016-2025 Fonte Concursos - Questões de Concurso e Plano de Estudo